
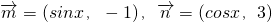 .
. 时,求
时,求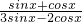 的值;
的值;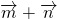 )•
)• ,求f(x)的单调增区间;
,求f(x)的单调增区间; c=2asin(A+B),对于(2)中的函数f(x),求f(B+
c=2asin(A+B),对于(2)中的函数f(x),求f(B+ )的取值范围.
)的取值范围.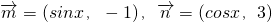 ,
,
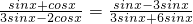 =-
=- ;
;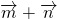 )•
)• =(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2
=(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2 +
+ sin2x-2=
sin2x-2= sin(
sin(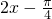 )-
)-
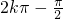 ≤
≤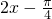 ≤
≤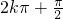 ,可得
,可得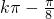 ≤x≤
≤x≤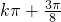
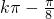 ,
,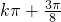 ](k∈Z);
](k∈Z); c=2asin(A+B),
c=2asin(A+B), sinC=2sinAsinC,
sinC=2sinAsinC,

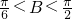
 )=
)= sin[2(B+
sin[2(B+ )-
)- ]-
]- =
= sin2B-
sin2B-
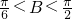 ,∴
,∴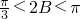
 <f(B+
<f(B+ )≤
)≤ -
- .
.

 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源:2009-2010学年山东省济宁一中高三(上)第一次反馈练习数学试卷(理科)(解析版) 题型:解答题
 ,
,
 时,求函数f(x)的值域;
时,求函数f(x)的值域; 个单位后,再将所得图象上各点向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的图象与直线
个单位后,再将所得图象上各点向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的图象与直线 以及x轴所围成的封闭图形的面积.
以及x轴所围成的封闭图形的面积.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌市高三第二次模拟测试理科数学试卷(解析版) 题型:解答题
已知向量

 ,
,
(1)当 时,求函数
时,求函数 的值域:
的值域:
(2)锐角 中,
中, 分别为角
分别为角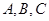 的对边,若
的对边,若 ,求边
,求边 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com