
【题目】对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】(2017安徽蚌埠一模)已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2
,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2![]() .
.

(1)求椭圆C的方程;
(2)设圆T:(x-2)2+y2=![]() ,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,不能证明AP⊥BC的条件是( )
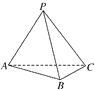
A. AP⊥PB,AP⊥PC
B. AP⊥PB,BC⊥PB
C. 平面BPC⊥平面APC,BC⊥PC
D. AP⊥平面PBC
查看答案和解析>>
科目:高中数学 来源: 题型:
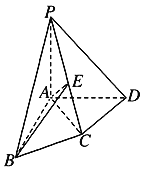
【题目】如图,在四棱锥![]() 中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
中,PA⊥平面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.证明:
(1)CD⊥AE;
(2)PD⊥平面ABE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,已知
中,已知![]() 分别为
分别为![]() 和
和![]() 的中点,对角线
的中点,对角线![]() 与
与![]() 交于
交于![]() 点,沿
点,沿![]() 把矩形
把矩形![]() 折起,使两个半平面所成二面角为60°,如图(2).
折起,使两个半平面所成二面角为60°,如图(2).

(1)求证:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新鲜的荔枝很好吃,但摘下后容易变黑,影响卖相.某大型超市进行扶贫工作,按计划每年六月从精准扶贫户中订购荔枝,每天进货量相同且每公斤20元,售价为每公斤24元,未售完的荔枝降价处理,以每公斤16元的价格当天全部处理完.根据往年情况,每天需求量与当天平均气温有关.如果平均气温不低于25摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温位于
公斤;如果平均气温位于![]() 摄氏度,需求量为
摄氏度,需求量为![]() 公斤;如果平均气温低于15摄氏度,需求量为
公斤;如果平均气温低于15摄氏度,需求量为![]() 公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
公斤.为了确定6月1日到30日的订购数量,统计了前三年6月1日到30日各天的平均气温数据,得到如图所示的频数分布表:
平均气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(Ⅰ)假设该商场在这90天内每天进货100公斤,求这90天荔枝每天为该商场带来的平均利润(结果取整数);
(Ⅱ)若该商场每天进货量为200公斤,以这90天记录的各需求量的频率作为各需求量发生的概率,求当天该商场不亏损的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击手在同一条件下进行射击训练,结果如下:
射击次数n | 10 | 20 | 50 | 100 | 200 | 500 |
击中靶心次数m | 8 | 19 | 44 | 92 | 178 | 455 |
击中靶心频率 |
(1)求出表中击中靶心的各个频率值;
(2)这个射击手射击一次,击中靶心的概率可估计为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)抛物线的开口向 、对称轴为直线 、顶点坐标 ;
(2)当![]() 时,函数有最 值,是 ;
时,函数有最 值,是 ;
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;当
的增大而增大;当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
(4)该函数图象可由![]() 的图象经过怎样的平移得到的?
的图象经过怎样的平移得到的?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求圆![]() 的直角坐标方程;
的直角坐标方程;
(II)若![]() 是直线
是直线![]() 与圆面
与圆面![]() 的公共点,求
的公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com