
| A. | $({1,\sqrt{2}})$ | B. | $(0,\sqrt{2}]$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({1,\sqrt{3}})$ |
分析 求出A的范围,由正弦定理可得 b=2cosA,从而得到 b 的取值范围.
解答 解:在锐角△ABC中,BC=1,∠B=2∠A,
∴$\frac{π}{2}$<3 A<π,且 0<2A<$\frac{π}{2}$,
故 $\frac{π}{6}$<A<$\frac{π}{4}$,
故 $\frac{\sqrt{2}}{2}$<cosA<$\frac{\sqrt{3}}{2}$.
由正弦定理可得 $\frac{1}{sinA}$=$\frac{b}{sin2A}$,
∴b=2cosA,
∴$\sqrt{2}$<b<$\sqrt{3}$,
故选:C
点评 本题考查锐角三角形的定义,正弦定理的应用,求得 $\frac{π}{6}$<A<$\frac{π}{4}$,是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | y′=2xcosx-x 2sinx | B. | y′=2xcosx+x 2sinx | ||
| C. | y′=x 2cosx-2xsinx | D. | y′=xcosx-x 2sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{1}{5}$i | C. | $\frac{1}{5}$-$\frac{3}{5}$i | D. | $\frac{3}{5}$-$\frac{1}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{7}}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
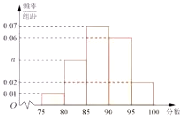 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:
某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示,其中成绩分组区间是:[75,80),[80,85),[85,90),[90,95),[95,100],规定90分及以上为合格:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com