
【题目】用“斜二测”画法画出△ABC(A为坐标原点,AB在x轴上)的直观图为△A′B′C′,则△A′B′C′的面积与△ABC的面积的比为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
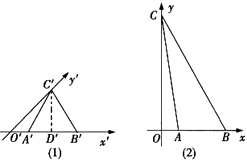
【解析】解:将△A'B'C'放入锐角为45°的斜角坐标系x'o'y'内,如图(1)所示,
过C'作C'D'⊥A'B',垂足为D',
将其还原为真实图形,得到图(2)的△ABC,
其中OA=O'A',AB=A'B',OC=2O'C',
在△OC'D'中,O'C'= ![]() =
= ![]() CD,即CD=
CD,即CD= ![]() O'C'=
O'C'= ![]() OC,
OC,
∴△ABC的高等于OC
由此可得△ABC的面积S= ![]() ABOC,
ABOC,
∵直观图中△A'B'C'的面积为S= ![]() AB
AB ![]() OC,
OC,
∴直观图和真实图形的面积的比值等于 ![]() ,
,
所以答案是:C.
【考点精析】利用平面图形的直观图和斜二测法画直观图对题目进行判断即可得到答案,需要熟知要画好对应平面图形的直观图,首先应在原图形中确定直角坐标系,然后在此基础上画出水平放置的平面坐标系;斜二测画法的步骤:(1)平行于坐标轴的线依然平行于坐标轴;(2)平行于y轴的线长度变半,平行于x,z轴的线长度不变;(3)画法要写好.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆 ![]() 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线 ![]() 的焦点,且椭圆
的焦点,且椭圆 ![]() 的离心率是
的离心率是 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过点 ![]() 的动直线与椭圆
的动直线与椭圆 ![]() 相交于
相交于 ![]() 两点.若线段
两点.若线段 ![]() 的中点的横坐标是
的中点的横坐标是 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y=ax2(a>0)的焦点到准线的距离为 ![]() ,且C上的两点A(x1 , y1),B(x2 , y2)关于直线y=x+m对称,并且
,且C上的两点A(x1 , y1),B(x2 , y2)关于直线y=x+m对称,并且 ![]() ,那么m= .
,那么m= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心在直线3x﹣y=0上且在第一象限,圆C与x相切,且被直线x﹣y=0截得的弦长为2 ![]() .
.
(1)求圆C的方程;
(2)若P(x,y)是圆C上的点,满足 ![]() x+y﹣m≤0恒成立,求m的范围.
x+y﹣m≤0恒成立,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在每年的春节后,某市政府都会发动公务员参与到植树绿化活动中去.林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)画出两组数据的茎叶图,并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为![]() ,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知中心在原点,焦点在x轴上的双曲线C的离心率为 ![]() ,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
,且双曲线C与斜率为2的直线l相交,且其中一个交点为P(﹣3,0).
(1)求双曲线C的方程及它的渐近线方程;
(2)求以直线l与坐标轴的交点为焦点的抛物线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知元素为实数的集合![]() 满足下列条件:①
满足下列条件:①![]() ,
, ![]() ;②若
;②若![]() ,则
,则![]() .
.
(I)若![]() ,求使元素个数最少的集合
,求使元素个数最少的集合![]() ;
;
(II)若非空集合![]() 为有限集,则你对集合
为有限集,则你对集合![]() 的元素个数有何猜测?并请证明你的猜测正确.
的元素个数有何猜测?并请证明你的猜测正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com