练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知⊙Ca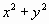：＋(a－2)x＋ay－2a＝0，其中aR．

    (1)证明⊙Ca过定点；(2)求圆心C的轨迹方程；(3)求面积最小的圆方程．

    答案：
    解析：

    		 (1)⊙ ： ＝0，解方程组

    (1)⊙：＝0，解方程组

    得定点(1，1)，(2，0)．

    (2)设圆心C(x，y)，则得参数方程

    (a为参数)

    消去参数a，得　x－y－1＝0．

    (3)⊙：＝，

    面积最小的圆，应当是a＝－1，故圆方程为

    ＝0．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：走向清华北大同步导读·高二数学(上) 题型：044

    已知双曲线C的虚轴长是8，两个顶点的坐标是(2，1)和(2，－5)，求双曲线及其渐近线的方程．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    已知⊙C：(x－3)2＋(y－4)2＝1，点A(－1，0)、B(1，0)，点P是圆上动点，求d＝|PA|2＋|PB|2的最大、最小值及对应的P坐标．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：044

    已知函数f(x)＝x(x－a)(x－b)，其中0＜a＜b．

    (1)设f(x)在x＝s及x＝t处取到极值，其中s＜t，求证：0＜s＜a＜t＜b．

    (2)设A(s，f(s))，B(t，f(t))，求证：线段AB的中点C在曲线y＝f(x)上．

    (3)若a＋b＜2，求证：过原点且与曲线y＝f(x)相切的两条直线不可能垂直．

    查看答案和解析>>

    科目：高中数学 来源：潮阳一中2007届高三摸底考试、理科数学 题型：044

    解答题

    已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点为圆心，1为半径为圆相切，又知C的一个焦点与A关于直线y＝x对称．

    (1)

    求双曲线C的方程；

    (2)

    若Q是双曲线C上的任一点，F1、F2为双曲线C的左、右两个焦点，从F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程．

    (3)

    设直线y＝mx＋1与双曲线C的左支交于A、B两点，另一直线L经过M(－2，0)及AB的中点，求直线L在y轴上的截距b的取值范围．

    查看答案和解析>>

    同步练习册答案