练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
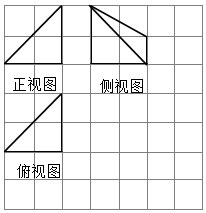
    10．某几何体的三视图如图所示，图中小方格的长度为1，则该几何体的体积为（　　）
    A．$\frac{8}{3}$B．4C．2D．$\frac{16}{3}$

    分析 根据三视图知几何体是四棱锥为棱长为2的正方体一部分，画出直观图，由正方体的性质判断出线面的位置关系，由椎体的体积公式求出该几何体的体积．

    解答 解：根据三视图知几何体是：
    四棱锥P-ABCD为棱长为2的正方体一部分，
    直观图如图所示：且D是棱的中点，
    由正方体的性质可得，PA⊥平面ABCD，
    ∴该几何体的体积V=$\frac{1}{3}×\frac{1}{2}×（1+2）×2×2$
    =2，
    故选：C．

    点评 本题考查由三视图求几何体的体积，在三视图与直观图转化过程中，以一个正方体为载体是很好的方式，使得作图更直观，考查空间想象能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016-2017学年江西吉安一中高二上段考一数学（文）试卷（解析版） 题型：选择题

    已知下列三个命题：

    ①棱长为2的正方体外接球的体积为；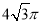

    ②如果将一组数据中的每一个数都加上同一个非零常数，那么这组数据的平均数和方差都改变；

    ③直线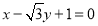被圆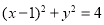截得的弦长为.

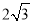    其中真命题的序号是（ ）

    A．①② B．②③ C. ①③ D．①②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图，斜三棱柱ABC-A1B1C1的底面是直角三角形，∠ACB=90°，点B1在底面ABC上的射影恰为BC的中点，且BC=CA=AA1．
    （Ⅰ）求证：平面ACC1A1⊥平面BCC1B1；
    （Ⅱ）求证：BC1⊥AB1；
    （Ⅲ）求二面角B-AB1-C1的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设函数f（x）=lnx+$\frac{m}{x}$，m∈R．
    （I）当m=1时，求f（x）的极小值；
    （Ⅱ）当0＜m＜$\frac{2}{3}$时，判断函数g（x）=f′（x）-$\frac{x}{3}$零点的个数；
    （Ⅲ）若h（x）=f（x）-x在（0，+∞）上单凋递减，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知一个几何体的三视图如图所示，则该几何体的体积为12+π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

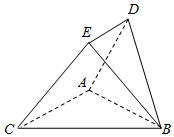    15．如图，以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直，且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$．
    （1）求证：平面EBC⊥平面ABC；
    （2）求二面角E-AC-B的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．讨论函数f（x）=（a-1）lnx+ax2+1的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知向量$\overrightarrow{a}$=（$\sqrt{3}$，sin4x），$\overrightarrow{b}$=（cos4x，1），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
    （1）求f（x）的最小正周期及最大值；
    （2）求f（x）的单调递增区间；
    （3）作f（x）在一个周期的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数f（x）=2-ax+1（a＞0且a≠1）的图象恒过定点（　　）
    A．（0，2）B．（1，2）C．（-1，1）D．（-1，2）

    查看答案和解析>>

    同步练习册答案