
【题目】设函数![]() ,其中
,其中![]() .
.
(![]() )若
)若![]() ,求函数
,求函数![]() 的单调递减区间.
的单调递减区间.
(![]() )求函数
)求函数![]() 的极值.
的极值.
(![]() )若函数
)若函数![]() 在区间
在区间![]() 上恰有两个零点,求
上恰有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,函数
时,函数![]() 无极值,当
无极值,当![]() 时,
时,![]() 的极大值为
的极大值为![]() ,无极小值;(3)
,无极小值;(3)![]() .
.
【解析】试题分析:(1)求出![]() ,在定义域内,分别令
,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)讨论当
的减区间;(2)讨论当![]() 时,当
时,当![]() 时,两种情况,分别判断导函数的符号,可得函数的单调区间,结合函数的单调性可得函数
时,两种情况,分别判断导函数的符号,可得函数的单调区间,结合函数的单调性可得函数![]() 的极值;(
的极值;(![]() )若
)若![]() 在
在![]() 恰有两个零点,则
恰有两个零点,则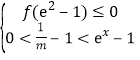 ,即
,即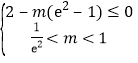 ,解得
,解得![]() .
.
试题解析:(![]() )依题意,函数
)依题意,函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ,又∵
,又∵![]() ,∴函数
,∴函数![]() 的单调递减区间是
的单调递减区间是![]() .
.
(![]() )
)![]() ,
,![]() ,当
,当![]() 时,
时,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 无极值,当
无极值,当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,∴
上单调递减,∴![]() ,无极小值, 综上所述,当
,无极小值, 综上所述,当![]() 时,函数
时,函数![]() 无极值,
无极值,
当![]() 时,
时,![]() 的极大值为
的极大值为![]() ,无极小值.
,无极小值.
(![]() )由(
)由(![]() )可知,当
)可知,当![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,显然,
上是增函数,显然,![]() 在区间
在区间![]() 不可能恰有两个零点,当
不可能恰有两个零点,当![]() 时,
时,![]() ,又
,又![]() , ∴
, ∴![]() 为
为![]() 的一个零点,∴若
的一个零点,∴若![]() 在
在![]() 恰有两个零点,则
恰有两个零点,则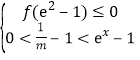 ,即
,即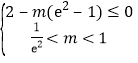 ,解得
,解得![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】对于每项均是正整数的数列A:a1,a2,…,an,定义变换T1,T1将数列A变换成数列T1(A):n,a1-1,a2-1,…,an-1.对于每项均是非负整数的数列B:b1,b2,…,bm,定义变换T2,T2将数列B各项从大到小排列,然后去掉所有为零的项,得到数列T2(B).又定义S(B)=2(b1+2b2+…+mbm)+![]() +
+![]() +…+
+…+![]() .设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
.设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
(1)如果数列A0为2,6,4,8,写出数列A1,A2;
(2)对于每项均是正整数的有穷数列A,证明:S(T1(A))=S(A);
(3)证明:对于任意给定的每项均为正整数的有穷数列A0,存在正整数K,当k≥K时,S(Ak+1)=S(Ak).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线后人称之为三角形的欧拉线.已知![]() 的顶点
的顶点![]() ,若其欧拉线方程为
,若其欧拉线方程为![]() ,则顶点C的坐标是()
,则顶点C的坐标是()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据市场调查发现,某种产品在投放市场的30天中,其销售价格![]() (元)和时间
(元)和时间![]() (天)的关系如图所示.
(天)的关系如图所示.

(1)求销售价格![]() (元)和时间
(元)和时间![]() (天)的函数关系式;
(天)的函数关系式;
(2)若日销售量![]() (件)与时间
(件)与时间![]() (天)的函数关系式是
(天)的函数关系式是![]()
![]() ,问该产品投放市场第几天时,日销售额
,问该产品投放市场第几天时,日销售额![]() (元)最高,且最高为多少元?
(元)最高,且最高为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2![]() ,AA1=
,AA1=![]() ,BB1=2
,BB1=2![]() ,点E和F分别为BC和A1C的中点.
,点E和F分别为BC和A1C的中点.

(1)求证:EF∥平面A1B1BA;
(2)求直线A1B1与平面BCB1所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com