已知函数f(x)=logax,g(x)=loga(2x+m-2),其中x∈[1,2],a>0且a≠1,m∈R.
(I)当m=4时,若函数F(x)=f(x)+g(x)有最小值2,求a的值;
(Ⅱ)当0<a<l时,f(x)≥2g(x)恒成立,求实数m的取值范围.
【答案】
分析:(I)将m=4代入F(x),求出其定义域,先判断其为增函数,根据题意函数F(x)=f(x)+g(x)有最小值2,列出等式,求a的值;
(Ⅱ)0<a<l,求出其定义域,可以令h(x)=4x
2+(4m-9)x+(m-2)
2,对其进行配方,分类讨论,求出h(x)的最小值,让其大于0即可求实数m的取值范围;
解答:解:(I)由题意,m=4时,F(x)=f(x)+g(x)=log
ax+log
a(2x+2)=
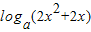
,
又x∈[1,2],则2x
2+2x∈[4,12].
而函数F(x)=f(x)+g(x)有最小值2,
∴a>1,解得a=2;
(Ⅱ)由题意,0<a<1时,∵f(x)≥2g(x),
∴
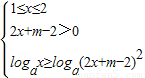
⇒
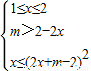
,
⇒

,
令h(x)=4x
2+(4m-9)x+(m-2)
2=4[x-(

-
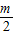
)]
2+(m-2)
2-
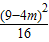
,
(1)当0<m<

时,1<

-
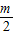
<
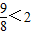
,
函数h(x)min=(m-2)
2-
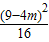
≥0,
解得m无解;
(2)当m≥

时,函数h(x)在x∈[1,2]上的单调递减,
则h(x)
min=h(1)=m
2-1≥0⇒m≥1.
综上,实数m的取值范围为[1,+∞).
点评:此题主要考查对数函数的性质及其应用,解题的过程中利用到了转化的思想,考查的知识点比较大,是一道难题;

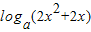 ,
,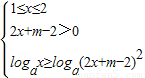
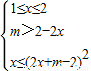 ,
, ,
, -
-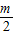 )]2+(m-2)2-
)]2+(m-2)2-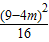 ,
, 时,1<
时,1< -
-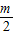 <
<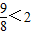 ,
,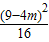 ≥0,
≥0, 时,函数h(x)在x∈[1,2]上的单调递减,
时,函数h(x)在x∈[1,2]上的单调递减,
