
【题目】对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的过焦点且垂直于对称轴的弦的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)
能使抛物线方程为y2=10x的条件是_____.
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
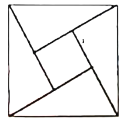
A.360种B.720种C.480种D.420种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,![]() E是PD的中点.
E是PD的中点.
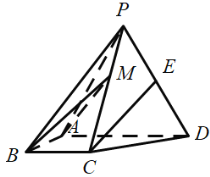
(1)证明:直线![]() 平面PAB;
平面PAB;
(2)点M在棱PC 上,且直线BM与底面ABCD所成角为![]() ,求二面角M-AB-D的余弦值.
,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过曲线C:y![]() x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
x2的焦点F,并与曲线C交于A(x1,y1),B(x2,y2)两点.
(1)求证:x1x2=﹣16;
(2)曲线C分别在点A,B处的切线(与C只有一个公共点,且C在其一侧的直线)交于点M,求点M的轨迹.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流![]() 类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:
类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)将同一组数据用该区间的中点值作代表,求这100人月薪收入的样本平均数![]() ;
;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设区间![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收取600元,月薪落在区间
内的每人收取600元,月薪落在区间![]() 右侧的每人收取800元;
右侧的每人收取800元;
方案二:每人按月薪收入的样本平均数的![]() 收取;
收取;
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]()
![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
,![]() 为垂足.当点
为垂足.当点![]() 在圆上运动时,线段
在圆上运动时,线段![]() 的中点
的中点![]() 形成轨迹
形成轨迹![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点,![]() 为曲线
为曲线![]() 上一动点,求
上一动点,求![]() 面积的最大值
面积的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com