
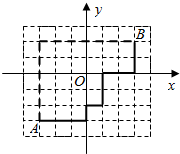
 现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.
现代城市大多是棋盘式布局(如上海道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1)、B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.分析 (1)由题意可得|x|+|y|=2,从而写出格点即可;
(2)设定点坐标为(a,b),定值为r,从而可得“圆”的方程为|x-a|+|y-b|=r,从而解得“圆”的方程为|x-2|+|y-2|=2,作其图象即可;
(3)由题意,B={(x,y)||x|+|y|≤1},从而可得|x-x1|+|y-y1|≤1,从而可得点集Q表示以点A内的点为定点,1为定长的“圆”及其内部,从而求面积.
解答 解:(1)(0,2)、(1,1)、(2,0)、(1,-1)、(0,-2)、(-1,-1)、(-2,0)、(-1,1);
(2)设定点坐标为(a,b),定值为r,
则“圆”的方程为|x-a|+|y-b|=r.
则$\left\{{\begin{array}{l}{|a-1|+|b-3|=r}\\{|a-1|+|b-1|=r}\\{|a-3|+|b-3|=r}\end{array}⇒\left\{{\begin{array}{l}{a=2}\\{b=2}\\{r=2}\end{array}}\right.}\right.$.
“圆”的方程为|x-2|+|y-2|=2.
作其图象如下,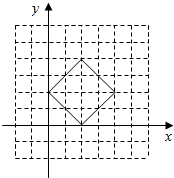 .
.
(3)B={(x,y)||x|+|y|≤1},
∵$\left\{\begin{array}{l}{x={x}_{1}+{x}_{2}}\\{y={y}_{1}+{y}_{2}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{2}=x-{x}_{1}}\\{{y}_{2}=y-{y}_{1}}\end{array}\right.$,
∵(x2,y2)∈B,
∴|x2|+|y2|≤1,
即|x-x1|+|y-y1|≤1,
∵点集A表示以原点为中心,边长为2的正方形及其内部,
∴点集Q表示以点A内的点为定点,1为定长的“圆”及其内部.
面积$S=4×4-\frac{1}{2}×1×1×4=14$.
点评 本题考查了学生的接受能力与应用能力,同时考查了学生的作图能力.


科目:高中数学 来源: 题型:填空题
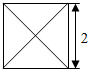 已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.
已知某几何体的俯视图是如图所示的边长为2的正方形,正视图与侧视图是边长为2的正三角形,则该几何体的体积是$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 7.5 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)
如图|$\overrightarrow{OA}|=|\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=5,则$\overrightarrow{OC}$=$\frac{10\sqrt{3}}{3}$$\overrightarrow{OA}$+$\frac{5\sqrt{3}}{3}$$\overrightarrow{OB}$.(用$\overrightarrow{OA}和\overrightarrow{OB}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=0 | B. | a≥$\frac{9}{8}$ | C. | a=0或a≥$\frac{9}{8}$ | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 37:8 | B. | 8:27 | C. | 27:64 | D. | 19:37 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com