
分析 (I)根据<$\sqrt{2}$>的定义和$\sqrt{2}$的范围依次计算a1,a2,a3,即可得出结论;
(II)根据定义可知$\frac{1}{2}<a<1$,依次计算a1,a2,列方程即可解出a的值.
解答 解:(I)∵1$<\sqrt{2}$<3,
∴a1=<$\sqrt{2}$>=$\sqrt{2}$-1,
∴$\frac{1}{{a}_{1}}$=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}+1$,
∵2$<\sqrt{2}+1<3$,
∴a2=<$\sqrt{2}+1$>=$\sqrt{2}+1-2$=$\sqrt{2}$-1,
同理可得:a3=a4=…=an=$\sqrt{2}-1$,
∴an=$\sqrt{2}$-1,
(II)∵a1=<a>=a,∴a<1,
又$a>\frac{1}{2}$,∴1$<\frac{1}{a}<2$,
∴a2=<$\frac{1}{{a}_{1}}$>=<$\frac{1}{a}$>=$\frac{1}{a}-1$,
∵a2=a,
∴$\frac{1}{a}-1=a$,解得a=$\frac{\sqrt{5}-1}{2}$.
故答案为(I)${a_n}=\sqrt{2}-1$,(II)$\frac{{\sqrt{5}-1}}{2}$.
点评 本题考查了对新定义的理解,数列的通项公式的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数g(x)是奇函数 | B. | 函数g(x)在区间[π,2π]上是增函数 | ||
| C. | 函数g(x)的最小正周期是4π | D. | 函数g(x)的图象关于直线x=π对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
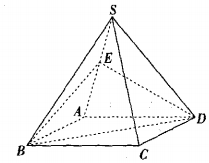 如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.
如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA的上一点,当点E满足条件SE=EA,时,SC∥平面EBD,写出条件并加以证明.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p为:?x∈(-2,2),|x-1|+|x+2|<6 | B. | ¬p为:?x∈(-2,2),|x-1|+|x+2|≥6 | ||
| C. | ¬p为:?x∈(-∞,-2]∪[2,+∞),|x-1|+|x+2|<6 | D. | ¬p为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com