
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(1)求![]() 的值;
的值;
(2)试推断方程![]() 是否有实数解?若有实数解,请求出它的解集.
是否有实数解?若有实数解,请求出它的解集.
【答案】(1)![]() ;(2)无实数解
;(2)无实数解
【解析】
(1)由题意,对函数f(x)=-x+lnx求导数,研究出函数在定义域上的单调性,判断出最大值,即可求出;
(2)由于函数的定义域是正实数集,故方程|2x(x-lnx)|=2lnx+x可变为![]() ,再分别研究方程两边对应函数的值域,即可作出判断.
,再分别研究方程两边对应函数的值域,即可作出判断.
(1)已知函数![]() ,则
,则![]() ,
,
可得![]() ,
,
令![]() ,x=1,
,x=1,
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数,
∴![]() ;
;
(2)|2x(xlnx)|=2lnx+x可得![]() ,
,
由(1)知f(x)max=f(1)=1,即x+lnx≤1,
∴|xlnx|≥1,
又令![]() ,
,![]() ,
,
令g′(x)>0,得0<x<e;令g′(x)<0,得x>e,
∴g(x)的增区间为(0,e),减区间为(e,+∞),
∴![]() ,∴g(x)<1,
,∴g(x)<1,
∴|xlnx|>g(x),即![]() 恒成立,
恒成立,
∴方程![]() 即方程|2x(xlnx)|=2lnx+x没有实数解.
即方程|2x(xlnx)|=2lnx+x没有实数解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“六艺”源于中国周朝的贵族教育体系,具体包括“礼、乐、射、御、书、数”.某校在周末学生业余兴趣活动中开展了“六艺”知识讲座,每艺安排一节,连排六节,则满足“礼”与“乐”必须排在前两节,“射”和“御”两讲座必须相邻的不同安排种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() _____.
_____.
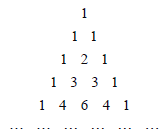
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(1)求椭圆C的方程;
(2)直线l交椭圆C于不同的两点A、B,且![]() 中点E在直线
中点E在直线![]() 上,线段
上,线段![]() 的垂直平分线交y轴于点
的垂直平分线交y轴于点![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列叙述:
①正四面体![]() 的棱长为
的棱长为![]() ,
,![]() 是棱
是棱![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的余弦值是
所成角的余弦值是![]() ;
;
②在等比数列![]() 中前
中前![]() 项和为
项和为![]() ,前
,前![]() 项和为
项和为![]() ,则前
,则前![]() 项和为
项和为![]() ;
;
③直线![]() 关于直线
关于直线![]() 对称的直线方程为
对称的直线方程为![]() ;
;
④若![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
其中所有正确叙述的序号是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行![]() 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标![]() 次的概率.
次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com