
【题目】设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c)(a﹣b+c)=ac. (Ⅰ)求B.
(Ⅱ)若sinAsinC= ![]() ,求C.
,求C.
【答案】解:(I)∵(a+b+c)(a﹣b+c)=(a+c)2﹣b2=ac, ∴a2+c2﹣b2=﹣ac,
∴cosB= ![]() =﹣
=﹣ ![]() ,
,
又B为三角形的内角,
则B=120°;
(II)由(I)得:A+C=60°,∵sinAsinC= ![]() ,cos(A+C)=
,cos(A+C)= ![]() ,
,
∴cos(A﹣C)=cosAcosC+sinAsinC=cosAcosC﹣sinAsinC+2sinAsinC=cos(A+C)+2sinAsinC= ![]() +2×
+2× ![]() =
= ![]() ,
,
∴A﹣C=30°或A﹣C=﹣30°,
则C=15°或C=45°
【解析】(I)已知等式左边利用多项式乘多项式法则计算,整理后得到关系式,利用余弦定理表示出cosB,将关系式代入求出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;(II)由(I)得到A+C的度数,利用两角和与差的余弦函数公式化简cos(A﹣C),变形后将cos(A+C)及2sinAsinC的值代入求出cos(A﹣C)的值,利用特殊角的三角函数值求出A﹣C的值,与A+C的值联立即可求出C的度数.
【考点精析】本题主要考查了两角和与差的正弦公式和余弦定理的定义的相关知识点,需要掌握两角和与差的正弦公式:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,a2=2,an+2=2an+1﹣an+2. (Ⅰ)设bn=an+1﹣an , 证明{bn}是等差数列;
(Ⅱ)求{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy内,动点P到定点F(﹣1,0)的距离与P到定直线x=﹣4的距离之比为 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设点A、B是轨迹C上两个动点,直线OA、OB与轨迹C的另一交点分别为A1、B1 , 且直线OA、OB的斜率之积等于- ![]() ,问四边形ABA1B1的面积S是否为定值?请说明理由.
,问四边形ABA1B1的面积S是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米. (Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y= ![]() (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( ) 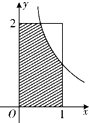
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】)已知命题p:“x∈[1,2],x2﹣a≥0”,命题q:“x∈R,x2+2ax+2﹣a=0”.若命题“p且q”是真命题,则实数a的取值范围为( )
A.﹣2≤a≤1
B.a≤﹣2或1≤a≤2
C.a≥1
D.a≤﹣2或 a=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() 的左焦点为F1 , 右焦点为F2 , 过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形.
的左焦点为F1 , 右焦点为F2 , 过F1的直线交椭圆于A,B两点,△ABF2的周长为8,且△AF1F2面积最大时,△AF1F2为正三角形. 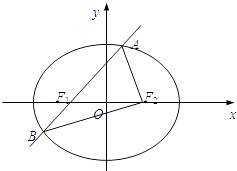
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:①以PQ为直径的圆与x轴的位置关系? ②在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出M的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com