[题目]已知点,.在抛物线上.的重心与此抛物线的焦点重合(I)写出该抛物线的方程和焦点的坐标,(II)求线段中点的坐标,(III)求弦所在直线的方程题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知点,，在抛物线上，的重心与此抛物线的焦点重合（如图）

（I）写出该抛物线的方程和焦点的坐标；

（II）求线段中点的坐标；

（III）求弦所在直线的方程

【答案】（1）抛物线方程为，焦点F的坐标为（8，0）。.

（2）M的坐标为（11，－4）。

（3）BC所在直线的方程为：

【解析】

解：（1）由点A（2，8）在抛物线上，有，

解得p="16." 所以抛物线方程为，焦点F的坐标为（8，0）

（2）由于F（8，0）是△ABC的重心，M是BC的中点，所以F分AM的比为2：1，即，设点M的坐标为，则

解得，所以点M的坐标为（11，－4）

（3）由于线段BC的中点M不在x轴上，所以BC所在

的直线不垂直于x轴.设BC所在直线的方程为：

由消x得，

所以，由（2）的结论得，解得

因此BC所在直线的方程为：

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．
（Ⅰ）求证：AB∥EF；
（Ⅱ）若PA=AD，且平面PAD⊥平面ABCD，求证：AF⊥平面PCD．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:

从甲城市2016年9月份的30天中随机抽取15天,这15天的PM2.5的日均浓度指数数据如茎叶图所示.

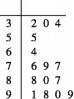
(1)试估计甲城市在2016年9月份的30天中,空气质量类别为优或良的天数;

(2)从甲城市的这15个监测数据中任取2个,设X是空气质量类别为优或良的天数,求X的分布列和数学期望.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，已知抛物线y2=2px（p＞0）上一点P（，m）到准线的距离与到原点O的距离相等，抛物线的焦点为F．
（1）求抛物线的方程；
（2）若A为抛物线上一点（异于原点O），点A处的切线交x轴于点B，过A作准线的垂线，垂足为点E．试判断四边形AEBF的形状，并证明你的结论．