
【题目】在标有“甲”的袋中有![]() 个红球和
个红球和![]() 个白球,这些球除颜色外完全相同.
个白球,这些球除颜色外完全相同.
(Ⅰ)若从袋中依次取出![]() 个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
(Ⅱ)现从甲袋中取出个![]() 红球,
红球, ![]() 个白球,装入标有“乙”的空袋.若从甲袋中任取
个白球,装入标有“乙”的空袋.若从甲袋中任取![]() 球,乙袋中任取
球,乙袋中任取![]() 球,记取出的红球的个数为
球,记取出的红球的个数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】某班共有学生45人,其中女生18人,现用分层抽样的方法,从男、女学生中各抽取若干学生进行演讲比赛,有关数据见下表(单位:人)
性别 | 学生人数 | 抽取人数 |
女生 | 18 |
|
男生 |
| 3 |
(1)求![]() 和
和![]() ;
;
(2)若从抽取的学生中再选2人做专题演讲,求这2人都是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x+ax2-2x,(a∈R,a≠0)
(1)若函数f(x)的图象在x=1处的切线与x轴平行,求f(x)的单调区间;
(2)若f(x)≤ax在x∈[![]() ,+∞)上恒成立,求a的取值范围.
,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.互相垂直的两条直线的直观图仍然是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面是边长为a的棱形,PD⊥底面ABCD.

(1)证明:AC⊥平面PBD;
(2)若PD=AD,直线PB与平面ABCD所成的角为45°,四棱锥P—ABCD的体积为![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验数据统计如下:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
A | 甲 | 4次 | 6次 | 2次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只要是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量ξ,求随机变量ξ的分布列和均值E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
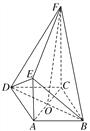
【题目】如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
(1)求证:BD⊥平面ACFE;
(2)当直线FO与平面BED所成的角为45°时,求异面直线OF与BE所成的角的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 若该大学某女生身高为170cm,则可断定其体重必为![]()
B. 回归直线过样本点的中心![]()
C. 若该大学某女生身高增加1cm,则其体重约增加![]()
D. y与x具有正的线性相关关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com