
【题目】某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(单位:分.百分制,均为整数)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
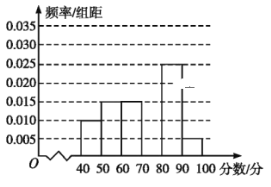
(1)求分数在![]() 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试成绩的众数和平均数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
【答案】(1)![]() ;作图见解析(2)众数:75;平均数:71(3)
;作图见解析(2)众数:75;平均数:71(3)![]()
【解析】
(1)由概率和为1直接计算即可求出分数在![]() 内的频率,即可直接补全频率分布直方图;
内的频率,即可直接补全频率分布直方图;
(2)直接观察频率分布直方图即可求得众数,再由平均数的计算公式即可求得平均数;
(3)由题意列出所有基本事件,找到符合要求的基本事件的个数即可得解.
(1)设分数在![]() 内的频率为
内的频率为![]() ,根据频率分布直方图,则有
,根据频率分布直方图,则有
![]() ,可得
,可得![]() .
.
则分数在![]() 内的频率为
内的频率为![]() ,频率分布直方图如下图:
,频率分布直方图如下图:

(2)由频率分布直方图可得众数为75;
平均数为![]()
![]() ,故平均数为71.
,故平均数为71.
(3)第1组:![]() 人(设为1,2,3,4,5,6),第6组:
人(设为1,2,3,4,5,6),第6组:![]() 人(设为
人(设为![]() ,
,![]() ,
,![]() ),
),
共有36个基本事件:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
满足条件的有18个,所以概率为![]() .
.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着甜品的不断创新,现在的甜品无论是造型还是口感都十分诱人,有颜值、有口味、有趣味的产品更容易得到甜品爱好者的喜欢,创新已经成为烘焙作品的衡量标准.某“网红”甜品店生产有几种甜品,由于口味独特,受到越来越多人的喜爱,好多外地的游客专门到该甜品店来品尝“打卡”,已知该甜品店同一种甜品售价相同,该店为了了解每个种类的甜品销售情况,专门收集了该店这个月里五种“网红甜品”的销售情况,统计后得如下表格:
甜品种类 | A甜品 | B甜品 | C甜品 | D甜品 | E甜品 |
销售总额(万元) | 10 | 5 | 20 | 20 | 12 |
销售额(千份) | 5 | 2 | 10 | 5 | 8 |
利润率 | 0.4 | 0.2 | 0.15 | 0.25 | 0.2 |
(利润率是指:一份甜品的销售价格减去成本得到的利润与该甜品的销售价格的比值.)
(1)从该甜品店本月卖出的甜品中随机选一份,求这份甜品的利润率高于0.2的概率;
(2)假设每类甜品利润率不变,销售一份A甜品获利![]() 元,销售一份B甜品获利
元,销售一份B甜品获利![]() 元,…,销售一份E甜品获利
元,…,销售一份E甜品获利![]() 元,设
元,设![]() ,若该甜品店从五种“网红甜品”中随机卖出2种不同的甜品,求至少有一种甜品获利超过
,若该甜品店从五种“网红甜品”中随机卖出2种不同的甜品,求至少有一种甜品获利超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax3+bx2+cx(a≠0)在x=±1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试判断x=±1是函数的极小值还是极大值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D为正三棱柱ABC﹣A1B1C1的棱AC的中点.
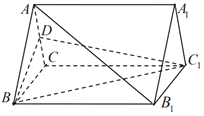
(1)证明:AB1∥平面BC1D
(2)若二面角C﹣BC1﹣D的大小为45°,求直线AB与平面BB1C1C夹角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=(3m2﹣2m)x![]() 在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
在(0,+∞)上单调递增,g(x)=x2﹣4x+t.
(1)求实数m的值;
(2)当x∈[1,9]时,记f(x),g(x)的值域分别为集合A,B,设命题p:x∈A,命题q:x∈B,若命题q是命题p的必要不充分条件,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com