
【题目】如图,在平面直角坐标系中,点F(﹣1,0),过直线l:x=﹣2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|= ![]() |BF|.
|BF|.
(1)求动点P的轨迹C的方程;
(2)过点F的直线q交曲线C于M,N,试问:x轴正半轴上是否存在点E,直线EM,EN分别交直线l于R,S两点,使∠RFS为直角?若存在,求出点E的坐标,若不存在,请说明理由.
【答案】
(1)解:设P(x,y),由平面几何知识得:
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
化简,得:x2+2y2=2,
∴动点P的轨迹C的方程为x2+2y2=2(x ![]() ).
).
(2)解:假设满足条件的点E(n,0)(n>0)存在,
设直线q的方程为x=my﹣1,
M(x1,y1),N(x2,y2),R(﹣2,y3),S(﹣2,y4),
联立 ![]() ,得:(m2+2)y2﹣2my﹣1=0,
,得:(m2+2)y2﹣2my﹣1=0,
y1+y2= ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
![]()
=﹣ ![]() +1=
+1= ![]() ,
,
![]() =﹣
=﹣ ![]() ,
,
由条件知 ![]() =
= ![]() ,y3=﹣
,y3=﹣ ![]() ,
,
同理 ![]() ,
,
![]() =﹣y3,kSF=﹣y4,
=﹣y3,kSF=﹣y4,
由于∠RFS为直角,∴y3y4=﹣1,即(2+n2)y1y2=﹣[x1x2+n(x1+x2)+n2],
(2+n)2 ![]() =
= ![]() +
+ ![]() +n2,
+n2,
∴(n2﹣2)(m2+1)=0,解得n= ![]() ,
,
∴满足条件的点E存在,其坐标为( ![]() ,0).
,0).
【解析】(1)设P(x,y),由平面几何知识得 ![]() =
= ![]() ,由此能求出动点P的轨迹C的方程.(2)假设满足条件的点E(n,0)(n>0)存在,设直线q的方程为x=my﹣1,联立
,由此能求出动点P的轨迹C的方程.(2)假设满足条件的点E(n,0)(n>0)存在,设直线q的方程为x=my﹣1,联立 ![]() ,得:(m2+2)y2﹣2my﹣1=0,由此利用韦达定理、直线方程、椭圆性质,结合已知条件能求出满足条件的点E存在,其坐标为(
,得:(m2+2)y2﹣2my﹣1=0,由此利用韦达定理、直线方程、椭圆性质,结合已知条件能求出满足条件的点E存在,其坐标为( ![]() ,0).
,0).


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】下列几个命题:
①函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
②方程![]() 的有一个正实根,一个负实根,
的有一个正实根,一个负实根,![]() ;
;
③![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]() 时,
时,![]()
④函数![]() 的值域是
的值域是![]() .
.
其中正确命题的序号是_____(把所有正确命题的序号都写上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 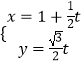 (为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线C2:
(为参数).在以坐标原点为极点,轴的正半轴为极轴的极坐标系中,曲线C2: ![]() . (Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
. (Ⅰ)求曲线C1的普通方程和C2的直角坐标方程;
(Ⅱ)若C1与C2相交于A、B两点,设点F(1,0),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(2)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的 ![]() 的值(
的值( ![]() 精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果:
精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果: 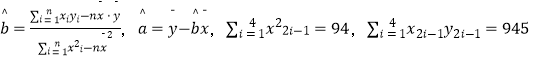 )
)
(3)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( ) 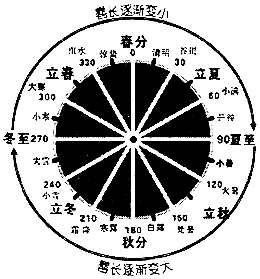
A.五寸
B.二尺五寸
C.三尺五寸
D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的左、右焦点分别为F1 , F2 , 过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )
=1(a>b>0)的左、右焦点分别为F1 , F2 , 过F2作一条直线(不与x轴垂直)与椭圆交于A,B两点,如果△ABF1恰好为等腰直角三角形,该直线的斜率为( )
A.±1
B.±2
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线E:x2=2py(p>0)焦点F且倾斜角的60°直线l与抛物线E交于点M,N,△OMN的面积为4.
(1)求抛物线E的方程;
(2)设P是直线y=﹣2上的一个动点,过P作抛物线E的切线,切点分别为A、B,直线AB与直线OP、y轴的交点分别为Q、R,点C、D是以R为圆心、RQ为半径的圆上任意两点,求∠CPD最大时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表:
使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 ![]() =
= ![]() x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
A.8年
B.9年
C.10年
D.11年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(x+1)﹣x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式 ![]() >1恒成立,则实数a的取值范围为( )
>1恒成立,则实数a的取值范围为( )
A.[15,+∞)
B.(﹣∞,15]
C.(12,30]
D.(﹣12,15]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com