Question

小红和小明相约去参加超市的半夜不打烊活动，两人约定凌晨0点到1点之间在超市门口相见，并且先到的必须等后到的人30分钟才可以进超市先逛．如果两个人出发是各自独立的，在0点到1点的各个时候到达的可能性是相等的．

（1）求两个人能在约定的时间内在超市门口相见的概率；

（2）超市内举行抽奖活动，掷一枚骰子，掷2次，如果出现的点数之和是5的倍数，则获奖．小红参与活动，她获奖的概率是多少呢？

Answer 1

考点：

几何概型；古典概型及其概率计算公式．

专题：

概率与统计．

分析：

（1）由题意知本题是一个几何概型，试验包含的所有事件是Ω={（x，y）|0＜x＜1，0＜y＜1}，做出事件对应的集合表示的面积，写出满足条件的事件是A={（x，y）|0＜x＜1，0＜y＜1，|x﹣y|＜}，算出事件对应的集合表示的面积，根据几何概型概率公式得到结果．

（2）掷一枚骰子，掷2次，两次的结果数之间没有关系，易得总结果数是36，点数之和为5的倍数的基本事件数用列举法列举出来即可．

解答：

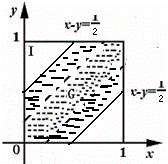
解：（1）设两人到达约会地点的时刻分别为x，y，依题意，必须满足|x﹣y|≤才能相遇．我们把他们到达的时刻分别作为横坐标和纵坐标，于是两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内，如图所示，而相遇现象则发生在阴影区域G内，即甲、乙两人的到达时刻（x，y）满足|x﹣y|≤，所以两人相遇的概率为区域G与区域Ⅰ的面积之比：P===．

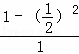也就是说，两个人能在约定的时间内在超市门口相见的概率为．

（2）设第一枚随机地投掷得到向上一面的点数为a，第二枚投掷得到向上一面的点数为b，则a与b的和共有36种情况． 

a b	1	2	3	4	5	6
1	（1，1）	（1，2）	（1，3）	（1，4）	（1，5）	（1，6）
2	（2，1）	（2，2）	（2，3）	（2，4）	（2，5）	（2，6）
3	（3，1）	（3，2）	（3，3）	（3，4）	（3，5）	（3，6）
4	（4，1）	（4，2）	（4，3）	（4，4）	（4，5）	（4，6）
5	（5，1）	（5，2）	（5，3）	（5，4）	（5，5）	（5，6）
6	（6，1）	（6，2）	（6，3）	（6，4）	（6，5）	（6，6）

所以两次取出的数字之和a+b是5的倍数的情况有（1，4），（4，1），（2，3），（3，2），（4，6），（6，4），（5，5），共7种，其概率为P=．

点评：

本题第一小问是一个几何概型，对于这样的问题，一般要通过把试验发生包含的事件同集合结合起来，根据集合对应的图形做出面积，用面积的比值得到结果．本题第二小问考查古典概率模型及其概率计算公式，求解关键是正确列举出事件A所包含的基本事件事，以及古典概率模型的计算公式．