
【题目】如图所示,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,AP=AD=2AB=2BC,点
,AP=AD=2AB=2BC,点![]() 在棱
在棱![]() 上.
上.
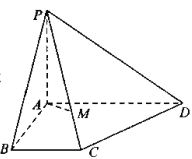
(Ⅰ)求证:![]() ;
;
(Ⅱ)当![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(I)设![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() .设出
.设出![]() 的边长,通过计算证明
的边长,通过计算证明![]() ,根据已知得到
,根据已知得到![]() ,由此证得
,由此证得![]() 平面
平面![]() ,从而证得
,从而证得![]() .(II)以
.(II)以![]() 为空间坐标原点建立空间直角坐标系,利用
为空间坐标原点建立空间直角坐标系,利用![]() 平面
平面![]() 计算出
计算出![]() 点的坐标,根据直线
点的坐标,根据直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量计算出线面角的正弦值.
的法向量计算出线面角的正弦值.
(Ⅰ)设![]() 中点为
中点为![]() ,连接
,连接![]() 、
、![]() .由题意
.由题意![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 为平行四边形,又
为平行四边形,又![]() ,∴
,∴![]() 为正方形.
为正方形.
设![]() ,在
,在![]() 中,
中,![]() ,又
,又![]() ,
,![]() .
.
∴![]() ,∴
,∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
(Ⅱ)因为![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,又
,又![]() ,故
,故![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() .
.
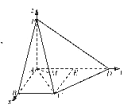
由(Ⅰ)所设知![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
由已知![]() 平面
平面![]() ,∴
,∴![]() ,设
,设![]() ,则
,则![]() .
.
![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.
设平面![]() 的法向量
的法向量![]() ,则
,则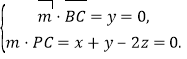
令![]() ,得
,得![]() .
.
设所求的角为![]() ,
,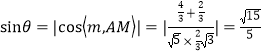 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】在圆周上依次有![]() 个点
个点![]() ,今随机地选取其中
,今随机地选取其中![]() 个点为顶点作凸
个点为顶点作凸![]() 边形
边形![]() ,已知选取与否的可能性是相同的,试求对每个
,已知选取与否的可能性是相同的,试求对每个![]() ,
,![]() 边形的两个相邻顶点
边形的两个相邻顶点![]() (规定
(规定![]() )之间至少有
)之间至少有![]() 中的
中的![]() 个点的概率,其中,
个点的概率,其中,![]() 是给定的一组正整数.
是给定的一组正整数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆锥形量杯的高为![]() 厘米,其母线与轴的夹角为
厘米,其母线与轴的夹角为![]() .
.

(1)求该量杯的侧面积![]() ;
;
(2)若要在该圆锥形量杯的一条母线![]() 上,刻上刻度,表示液面到达这个刻度时,量杯里的液体的体积是多少.当液体体积是
上,刻上刻度,表示液面到达这个刻度时,量杯里的液体的体积是多少.当液体体积是![]() 立方厘米时,刻度的位置
立方厘米时,刻度的位置![]() 与顶点
与顶点![]() 之间的距离是多少厘米(精确到
之间的距离是多少厘米(精确到![]() 厘米)?
厘米)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一袋中有标有号码1、2、3、4的卡片各一张,每次从中取出一张,记下号码后放回,当四种号码的卡片全部取出时即停止,则恰好取6次卡片时停止的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体的8个顶点、12条棱的中点、6个侧面的中心点、1个体的中心点,这27个点中,共球面的8点组的个数是().
A. 4462 B. 4584 C. 4590 D. 4602
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com