
【题目】已知函数![]() 是定义域为
是定义域为![]() 的偶函数,当
的偶函数,当![]() 时,
时, ,若关于
,若关于![]() 的方程
的方程![]()
![]() 有且仅有6个不同实数根,则实数
有且仅有6个不同实数根,则实数![]() 的取值范围为______.
的取值范围为______.
【答案】0<a≤![]() 或a
或a![]() .
.
【解析】
运用偶函数的性质,作出函数f(x)的图象,由5[f(x)]2﹣(5a+4)f(x)+4a=0,解得f(x)=a或f(x)![]() ,结合图象,分析有且仅有6个不同实数根的a的情况,即可得到a的范围.
,结合图象,分析有且仅有6个不同实数根的a的情况,即可得到a的范围.
函数![]() 是定义域为
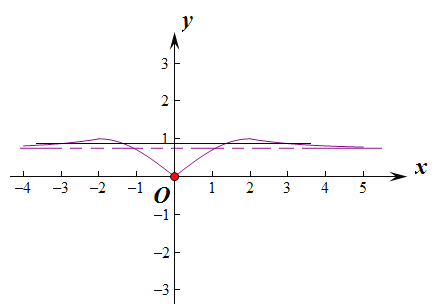
是定义域为![]() 的偶函数,作出函数f(x)的图象如图:
的偶函数,作出函数f(x)的图象如图:
关于x的方程5[f(x)]2﹣(5a+4)f(x)+4a=0,
解得f(x)=a或f(x)![]() ,
,
当0≤x≤2时,f(x)∈[0,![]() ],x>2时,f(x)∈(
],x>2时,f(x)∈(![]() ,
,![]() ).
).
由![]() ,则f(x)
,则f(x)![]() 有4个实根,
有4个实根,
由题意,只要f(x)=a有2个实根,
则由图象可得当0<a≤![]() 时,f(x)=a有2个实根,
时,f(x)=a有2个实根,
当a![]() 时,f(x)=a有2个实根.
时,f(x)=a有2个实根.
综上可得:0<a≤![]() 或a
或a![]() .
.
故答案为:0<a≤![]() 或a
或a![]() ..
..


科目:高中数学 来源: 题型:
【题目】在下列命题中:
①方程![]() 表示的曲线所围成区域面积为
表示的曲线所围成区域面积为![]() ;
;
②与两坐标轴距离相等的点的轨迹方程为![]() ;
;
③与两定点![]() 距离之和等于
距离之和等于![]() 的点的轨迹为椭圆;
的点的轨迹为椭圆;
④与两定点![]() 距离之差的绝对值等于1的点的轨迹为双曲线.
距离之差的绝对值等于1的点的轨迹为双曲线.
正确的命题的序号是________.(注:把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区上年度电价为![]() 元/kWh,年用电量为
元/kWh,年用电量为![]() kWh.本年度计划将电价降低到0.55元/ kWh到0.75元/ kWh之间,而用户期望电价为0.40元/ kWh.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为
kWh.本年度计划将电价降低到0.55元/ kWh到0.75元/ kWh之间,而用户期望电价为0.40元/ kWh.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为![]() ),该地区电力的成本价为0.30元/ kWh.
),该地区电力的成本价为0.30元/ kWh.
(1)写出本年度电价下调后,电力部门的收益![]() 与实际电价
与实际电价![]() 之间的函数关系式;
之间的函数关系式;
(2)设![]() =
=![]() ,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价-成本价))
,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价-成本价))
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在定义域内存在实数![]() ,使得
,使得![]() 成立,则称函数有“和一点”
成立,则称函数有“和一点”![]() .
.
(1)函数![]() 是否有“和一点”?请说明理由;
是否有“和一点”?请说明理由;
(2)若函数![]() 有“和一点”,求实数
有“和一点”,求实数![]() 的取值范围;
的取值范围;
(3)求证:![]() 有“和一点”.
有“和一点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 的底面边长和侧棱长均为2,
的底面边长和侧棱长均为2,![]() 为棱
为棱![]() 的中点 .
的中点 .
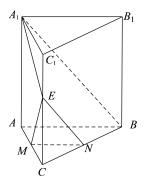
(1)证明:平面![]() 平面
平面![]() ;
;
(2)是否存在平行于![]() 的动直线
的动直线![]() ,分别与棱
,分别与棱![]() 交于点
交于点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若存在,求出点
,若存在,求出点![]() 到直线
到直线![]() 的距离;若不存在,说明理由.
的距离;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() 与
与![]() 相交于点M.设
相交于点M.设![]() ,
,![]() .
.

(1)试用向量![]() 表示
表示![]() .
.
(2)在线段![]() 上取点E,在线段
上取点E,在线段![]() 取点F,使
取点F,使![]() 过点M.设
过点M.设![]() ,
,![]() ,其中
,其中![]() 当
当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() ;当
;当![]() 与
与![]() 重合时,
重合时,![]() ,
,![]() ,此时
,此时![]() .能否由此得出般结论:不论
.能否由此得出般结论:不论![]() 在线段
在线段![]() 上如何变动,等式
上如何变动,等式![]() 恒成立,请说明理由.
恒成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com