
【题目】已知向量 ![]() ,将函数
,将函数 ![]() 的图象按向量
的图象按向量 ![]() 平移后得到函数g(x)的图象.
平移后得到函数g(x)的图象.
(1)求函数g(x)的表达式;
(2)若函数 ![]() 上的最小值为h(a),求h(a)的最大值.
上的最小值为h(a),求h(a)的最大值.
【答案】
(1)解:设P(x,y)是函数y=f(x)图象上的任意一点,它在函数y=g(x)图象上的对应点P'(x',y'),则由平移公式,得
∴ 代入函数 中,
得
∴函数y=g(x)的表达式为
(2)解:函数g(x)的对称轴为
①当 即 时,函数g(x)在[ ]上为增函数,
∴ ;
②当 即 时,
∴
当且仅当 时取等号;
③当 即 时,函数g(x)在[ ]上为减函数,
∴
综上可知,
∴当 时,函数h(a)的最大值为
【解析】(1)利用图象平移的知识,根据向量平移的公式建立平移之后的图象上点的坐标与平移之前图象上点的坐标之间的关系是解决本题的关键;(2)利用(1)中得到的函数关系式,确定该函数是二次函数类型,根据对称轴与函数定义区间的关系,结合分类讨论思想求出函数的最小值的表达式是解决本题的关键.
【考点精析】通过灵活运用函数的最值及其几何意义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值即可以解答此题.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知全集为实数集R,集合A={x|y= ![]() +
+ ![]() },B={x|log2x>1}.
},B={x|log2x>1}.
(1)分别求A∩B,(RB)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校要从参加数学竞赛的1000名学生中,随机抽取50名学生的成绩进行分析,现将参加数学竞赛的1000名学生编号如下000,001,002,…,999,如果在第一组随机抽取的一个号码为015,则抽取的第40个号码为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高三年级学生寒假期间的学习情况,某学校抽取了甲、乙两班作为对象,调查这两个班的学生在寒假期间平均每天学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生平均每天学习时间在区间![]() 的有8人.
的有8人.
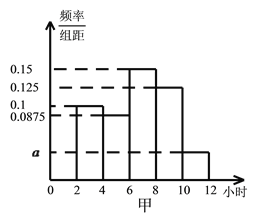

(I)求直方图中![]() 的值及甲班学生平均每天学习时间在区间
的值及甲班学生平均每天学习时间在区间![]() 的人数;
的人数;
(II)从甲、乙两个班平均每天学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com