
分析 (1)利用指数数列的定义,判断即可;
(2)求出{an}的通项公式为${a_n}={2^n}$,即可证明:{an}是指数数列;
(3)利用反证法进行证明即可.
解答 (1)解:对于数列{an},因为a3=a1+2≠a1•a2,所以{an}不是指数数列. …(2分)
对于数列{bn},对任意n,m∈N*,因为${b_{n+m}}={3^{n+m}}={3^n}•{3^m}={b_n}•{b_m}$,
所以{bn}是指数数列. …(4分)
(2)证明:由题意,an+2-an+1=2(an+1-an),
所以数列{an+1-an}是首项为a2-a1=2,公比为2的等比数列. …(2分)
所以${a_{n+1}}-{a_n}={2^n}$.所以,${a_n}=({a_n}-{a_{n-1}})+({a_{n-1}}-{a_{n-2}})+…+({a_2}-{a_1})+{a_1}={2^{n-1}}+{2^{n-2}}+…+2+2$
=$\frac{{2(1-{2^{n-1}})}}{1-2}+2={2^n}$,即{an}的通项公式为${a_n}={2^n}$(n∈N*). …(5分)
所以${a_{n+m}}={2^{n+m}}={2^n}•{2^m}={a_n}•{a_m}$,故{an}是指数数列. …(6分)
(3)证明:因为数列{an}是指数数列,故对于任意的n,m∈N*,有an+m=an•am,令m=1,则${a_{n+1}}={a_n}•{a_1}=\frac{t+3}{t+4}•{a_n}$,所以{an}是首项为$\frac{t+3}{t+4}$,公比为$\frac{t+3}{t+4}$的等比数列,
所以,${a_n}={({\frac{t+3}{t+4}})^n}$. …(2分)
假设数列{an}中存在三项au,av,aw构成等差数列,不妨设u<v<w,
则由2av=au+aw,得$2{({\frac{t+3}{t+4}})^v}={({\frac{t+3}{t+4}})^u}+{({\frac{t+3}{t+4}})^w}$,
所以2(t+4)w-v(t+3)v-u=(t+4)w-u+(t+3)w-u,…(3分)
当t为偶数时,2(t+4)w-v(t+3)v-u是偶数,而(t+4)w-u是偶数,(t+3)w-u是奇数,
故2(t+4)w-v(t+3)v-u=(t+4)w-u+(t+3)w-u不能成立; …(5分)
当t为奇数时,2(t+4)w-v(t+3)v-u是偶数,而(t+4)w-u是奇数,(t+3)w-u是偶数,
故2(t+4)w-v(t+3)v-u=(t+4)w-u+(t+3)w-u也不能成立.…(7分)
所以,对任意t∈N*,2(t+4)w-v(t+3)v-u=(t+4)w-u+(t+3)w-u不能成立,
即数列{an}的任意三项都不成构成等差数列. …(8分)
点评 本题考查指数数列的定义,考查反证法的运用,正确理解与运用新定义是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于$\frac{{\sqrt{6}}}{3}$.
三条侧棱两两垂直的正三棱锥,其俯视图如图所示,主视图的边界是底边长为2的等腰三角形,则主视图的面积等于$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
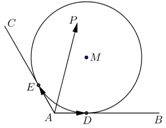 如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )
如图所示,∠BAC=$\frac{2π}{3}$,圆M与AB,AC分别相切于点D,E,AD=1,点P是圆M及其内部任意一点,且$\overrightarrow{AP}=x\overrightarrow{AD}+y\overrightarrow{AE}$(x,y∈R),则x+y的取值范围是( )| A. | $[1,4+2\sqrt{3}]$ | B. | $[4-2\sqrt{3},4+2\sqrt{3}]$ | C. | $[1,2+\sqrt{3}]$ | D. | $[2-\sqrt{3},2+\sqrt{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13.59% | B. | 15.73% | C. | 27.18% | D. | 31.46% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com