
分析 先分析题目中对于任意的x1∈D,存在唯一的x2∈D,使$\sqrt{f({x_1})f({x_2})}=3$成立,
再对题目中的函数进行分析、判断,得出符合条件的函数即可.
解答 解:根据题意可知:
对于(1),函数f(x)=3lnx,x=1时,lnx没有倒数,不成立;
对于(2),函数f(x)=3x2+1,当x1=0时,存在x2=±$\frac{2}{3}$$\sqrt{6}$使得使$\sqrt{f({x_1})f({x_2})}=3$,故不符合题意;
对于(3),函数f(x)=3ex,对任意一个自变量x,函数f(x)都有倒数,且使$\sqrt{f({x_1})f({x_2})}=3$成立;
对于(4),函数f(x)=$\frac{1}{x}$,对定义域内的任意一个自变量x,函数f(x)都有倒数,且使$\sqrt{f({x_1})f({x_2})}=3$成立;
所以成立的函数序号为(3)、(4).
故答案为:(3)、(4).
点评 本题主要应用新定义的方式考查均值不等式在函数中的应用问题,对于新定义的问题,需要认真分析定义内容,是易错题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
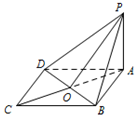
| A. | PD⊥CD | B. | BD⊥平面PAO | C. | PB⊥CB | D. | BC∥平面PAD |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 每件产品A | 每件产品B | ||
| 研制成本、搭载 费用之和(万元) | 20 | 30 | 计划最大资金额 300万元 |
| 产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元) | 80 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-3+\sqrt{17},+∞)$ | B. | $(3+\sqrt{17},+∞)$ | C. | $(-3+\sqrt{17},3+\sqrt{17})$ | D. | $(0,-3+\sqrt{17})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com