
【题目】下列函数是偶函数且在区间(0,+∞)上是增函数的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E、F分别是AB、CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF,如图2.
(1)当AG+GC最小时,求证:BD⊥CG;
(2)当2VB﹣ADGE=VD﹣GBCF时,求二面角D﹣BG﹣C平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,f (x)=sin(2x﹣A) (x∈R),函数f(x)的图象关于点( ![]() ,0)对称.
,0)对称.
(1)当x∈(0, ![]() )时,求f (x)的值域;
)时,求f (x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=![]() +a
+a![]() +a
+a![]() .
.
(1)设t=![]() ,求t的取值范图;
,求t的取值范图;
(2)把f(x)表示为t的函数h(t);
(3)设f (x)的最大值为M(a),最小值为m(a),记g(a)=M(a)-m(a)求g(a)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2(ex+e﹣x)﹣(2x+1)2(e2x+1+e﹣2x﹣1),则满足f(x)>0的实数x的取值范围为( )
A.(﹣1,﹣ ![]() )
)
B.(﹣∞,﹣1)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣∞,﹣1)∪(﹣ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司采用招考方式引进人才,规定必须在![]() ,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点
,三个测试点中任意选取两个进行测试,若在这两个测试点都测试合格,则可参加面试,否则不被录用,已知考生在每测试个点测试结果互不影响,若考生小李和小王一起前来参加招考,小李在测试点![]() 测试合格的概率分别为
测试合格的概率分别为![]() ,小王在上述三个测试点测试合格的概率都是
,小王在上述三个测试点测试合格的概率都是![]() .
.
(1)问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大?请说明理由;
(2)假设小李选择测试点![]() 进行测试,小王选择测试点
进行测试,小王选择测试点![]() 进行测试,记
进行测试,记![]() 为两人在各测试点测试合格的测试点个数之和,求随机变量
为两人在各测试点测试合格的测试点个数之和,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是平行四边形,
是平行四边形, ![]() 且
且![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
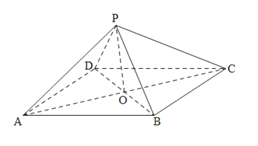
(1)![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)求证: 平面![]() 平面
平面![]() ;
;
(3)若![]() ,
, ![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为R,并且满足f(x+y)=f(x)+f(y),f(![]() )=1,当x>0时,f(x)>0.
)=1,当x>0时,f(x)>0.
(1)求f(0)的值;
(2)判断函数的奇偶性;
(3)如果f(x)+f(2+x)<2,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com