
【题目】已知数列![]() ,
, ![]() 满足
满足![]() ,
, ![]() ,且
,且![]() ,
, ![]() .
.
(1)求![]() 及
及![]() ;
;
(2)猜想![]() ,
, ![]() 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(3)证明:对所有的![]() ,
, 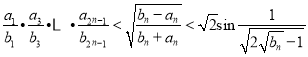 .
.
【答案】(1)![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)依次把n=1,2,3代入递推式即可求出{an},{bn}的前4项;
(2)利用数学归纳法证明猜想;
(3)利用放缩法证明不等式左边,利用函数单调性证明不等式右边.
试题解析:
(1)因为![]() ,
, ![]() ,且
,且![]() ,
,
令![]() ,得到
,得到![]() 解得
解得![]() ,
, ![]() ;同理令
;同理令![]() 分别解得由此可得
分别解得由此可得![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
;
(2)证明:猜测![]() ,
, ![]() ,
,
用数学归纳法证明:①当![]() 时,由上可得结论成立.
时,由上可得结论成立.
②假设当![]() 时,结论成立,即
时,结论成立,即![]() ,
, ![]() ,
,
那么当![]() 时,
时, ![]() ,
,
![]() ,所以当
,所以当![]() 时,结论也成立.
时,结论也成立.
由①②,可知![]() ,
, ![]() 对一切正整数都成立.
对一切正整数都成立.
(3)由(2)知, ![]() ,
,
于是所证明的不等式即为![]()
(ⅰ)先证明: ![]()
因为![]() ,所以
,所以![]() ,从而
,从而![]() ,
,
即![]() ,所以
,所以![]()
(ⅱ)再证明![]()
![]()
设函数![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
因为在区间![]() 上
上![]() 为增函数,
为增函数,
所以当![]() 时,
时, ![]() ,
,
从而![]() 在区间
在区间![]() 上为单调递减函数,
上为单调递减函数,
因此![]() 对于一切
对于一切![]() 都成立,因为当
都成立,因为当![]() 时,
时, ![]() ,
,
所以![]()
![]()
综上所述,对所有的![]() ,均有
,均有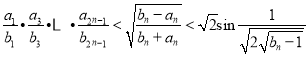 成立.
成立.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数),若
为参数),若![]() 是圆
是圆![]() 与
与![]() 轴正半轴的交点,以坐标原点
轴正半轴的交点,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,设过点
轴正半轴为极轴,建立极坐标系,设过点![]() 的圆
的圆![]() 的切线为
的切线为![]() .
.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)求圆![]() 上到直线
上到直线![]() 的距离最大的点的直角坐标.
的距离最大的点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.
(1)求实数m的取值范围;
(2)求该圆的半径r的取值范围;
(3)求圆心C的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是 ( )
A. 某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人
B. 两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180°
C. 由平面三角形的性质,推测空间四边形的性质
D. 在数列{an}中,a1=1,an=![]() (an-1+
(an-1+![]() )(n≥2),由此归纳出{an}的通项公
)(n≥2),由此归纳出{an}的通项公
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com