
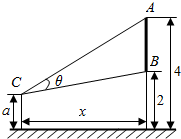
 如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.
如图,墙上有一壁画,最高点A离地面4米,最低点B离地面2米.观察者从距离墙x(x>1)米,离地面高a(1≤a≤2)米的C处观赏该壁画,设观赏视角∠ACB=θ.分析 (1)首项利用两角和的正切公式建立函数关系,进一步利用判别式确定函数的最大值;
(2)利用两角和的正切公式建立函数关系,利用a的取值范围即可确定x的范围.
解答  解:(1)如图,作CD⊥AF于D,则CD=EF,
解:(1)如图,作CD⊥AF于D,则CD=EF,
设∠ACD=α,∠BCD=β,CD=x,则θ=α-β,
在Rt△ACD和Rt△BCD中,tanα=$\frac{2.5}{x}$,tanβ=$\frac{0.5}{x}$,
则tanθ=tan(α-β)=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{2x}{{x}^{2}+1.25}$(x>0),
令u=$\frac{2x}{{x}^{2}+1.25}$,则ux2-2x+1.25u=0,
∵上述方程有大于0的实数根,∴△≥0,
即4-4×1.25u2≥0,∴u≤$\sqrt{\frac{1}{1.25}}$,即(tanθ)max=$\sqrt{\frac{1}{1.25}}$,
∵正切函数y=tanx在(0,$\frac{π}{2}$)上是增函数,
∴视角θ同时取得最大值,
此时,x=$\frac{2}{2u}$=$\sqrt{1.25}$,
∴观察者离墙$\sqrt{1.25}$米远时,视角θ最大;
(2)由(1)可知,tanθ=$\frac{1}{2}$=$\frac{\frac{4-a}{x}-\frac{2-a}{x}}{1+\frac{4-a}{x}•\frac{2-a}{x}}$=$\frac{2x}{{x}^{2}+8-6a+{a}^{2}}$,
即x2-4x+4=-a2+6a-4,
∴(x-2)2=-(a-3)2+5,
∵1≤a≤2,
∴1≤(x-2)2≤4,
化简得:0≤x≤1或3≤x≤4,
又∵x>1,
∴3≤x≤4.
点评 本题考查应用两角和的正切公式及其函数的单调性与最值,注意解题方法的积累,属于中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{5}{4}$) | B. | ($\frac{1}{2}$,-$\frac{5}{4}$) | C. | (-$\frac{1}{2}$,-$\frac{5}{4}$) | D. | ($\frac{1}{2}$,$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com