
分析 (1)由题意f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+2,根据平面向量数量积运算求解出f(x)化简,结合三角函数的性质即可求解.
(2)三角函数的图象和性质,出内层函数的单调减区间,x∈[0,2π]时,即得到f(x)的单调减区间.
解答 解:向量$\overrightarrow{a}$=($\frac{1}{2}$,$\frac{{\sqrt{3}}}{2}$),$\overrightarrow{b}$=(sinx,cosx),
由f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+2
=$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx+2
=sin(x+$\frac{π}{3}$)+2
根据三角函数的图象和性质:
当x+$\frac{π}{3}$=$\frac{π}{2}+2kπ$时,(k∈Z)
函数f(x)取得最大值3,此时x的集合为$\left\{{x\left|{x=2kπ+\frac{π}{6},k∈z}\right.}\right\}$
当x+$\frac{π}{3}$=-$\frac{π}{2}+2kπ$时,(k∈Z)
函数f(x)取得最小值1,此时x的集合为$\left\{{x\left|{x=2kπ-\frac{5π}{6},k∈z}\right.}\right\}$
(2)由(1)可得f(x)=sin(x+$\frac{π}{3}$)+2
由$\frac{π}{2}+2kπ$≤x+$\frac{π}{3}$≤$\frac{3π}{2}$+2kπ,(k∈Z)
解得:$2kπ+\frac{π}{6}$≤x≤$\frac{7π}{6}$+2kπ,(k∈Z)
∵x∈[0,2π]
∴单调减区间为$[{\frac{π}{6},\frac{7π}{6}}]$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [1,+∞) | C. | $[{-1,-\frac{3}{4}})$ | D. | $({\frac{3}{4},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
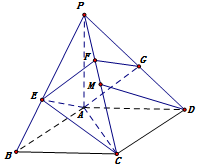 如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.
如图,PA垂直于矩形ABCD所在平面,AE⊥PB,垂足为E,EF⊥PC垂足为F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com