
【题目】某校从参加高三年级期中考试的学生中随机统计了40名学生的政治成绩,这40名学生的成绩全部在40分至100分之间,据此绘制了如图所示的样本频率分布直方图.

(1)求成绩在[80,90)的学生人数;
(2)从成绩大于等于80分的学生中随机选2名学生,求至少有1 名学生成绩在[90,100]的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据频率直方图可知其频率为![]() ,计算学生人数;(2) 设
,计算学生人数;(2) 设![]() 表示事件“在成绩大于等于
表示事件“在成绩大于等于![]() 分的学生中随机选两名学生,至少有
分的学生中随机选两名学生,至少有![]() 名学生成绩在区间
名学生成绩在区间![]() 内”,由已知和(1)的结果可知成绩在区间
内”,由已知和(1)的结果可知成绩在区间![]() 内的学生有
内的学生有![]() 人,记这四个人分别为
人,记这四个人分别为![]() ,成绩在区间
,成绩在区间![]() 内的学生有
内的学生有![]() 人,记这两个人分别为
人,记这两个人分别为![]() ,分别写出事件空间及事件,得到概率.
,分别写出事件空间及事件,得到概率.
试题解析:(1)因为各组的频率之和为1,所以成绩在区间[80,90)的频率为
1-(0.005×2+0.015+0.020+0.045)×10=0.1,
所以,40名学生中成绩在区间[80,90)的学生人数为40×0.1=4(人).
(2)设A表示事件“在成绩大于等于80分的学生中随机选两名学生,至少有1名学生成绩在区间[90,100]内”,
由已知和(1)的结果可知成绩在区间[80,90)内的学生有4人,记这四个人分别为a,b,c,d,成绩在区间[90,100]内的学生有2人,记这两个人分别为e,f,则选取学生的所有可能结果为:
(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),基本事件数为15,事件“至少1名学生成绩在区间[90,100]内”的可能结果为:
(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f),基本事件数为9,所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,
的左、右焦点, ![]() 为双曲线的左顶点,以
为双曲线的左顶点,以![]() ,
, ![]() 为直径的圆交双曲线某条渐近线于
为直径的圆交双曲线某条渐近线于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,则该双曲线的离心率为________.
,则该双曲线的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合P={(x,y)||x|+|y|≤1,x∈R,y∈R},Q={(x,y)|x2+y2≤1,x∈R,y∈R},R={(x,y)|x4+y2≤1,x∈R,y∈R}则下列判断正确的是( )
A.PQR
B.PRQ
C.QPR
D.RPQ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知直线![]() 与双曲线
与双曲线![]() 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求![]() 的值及B点坐标;
的值及B点坐标;
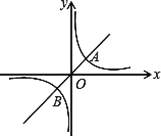
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)问题发现
如下图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE。
填空:①∠AEB的度数为____________;
②线段AD、BE之间的数量关系是_________。

(2)拓展探究
如下图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE。请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由。

(3)解决问题
如下图,在正方形ABCD中,CD=![]() 。若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。
。若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=cos2x﹣ ![]() sin2x,把y=f(x)的图象向左平移φ(φ>0)个单位后,恰好得到函数g(x)=﹣cos2x﹣
sin2x,把y=f(x)的图象向左平移φ(φ>0)个单位后,恰好得到函数g(x)=﹣cos2x﹣ ![]() sin2x的图象,则φ的值可以为( )
sin2x的图象,则φ的值可以为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2,连结
,如图2,连结![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},an≥0,a1=0,an+12+an+1﹣1=an2(n∈N).记Sn=a1+a2+…+an . Tn= ![]() +
+ ![]() +…+
+…+ ![]() .求证:当n∈N*时
.求证:当n∈N*时
(1)0≤an<an+1<1;
(2)Sn>n﹣2;
(3)Tn<3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com