
【题目】(2015·四川)已知函数f(x)=-2(x+a)lnx+x2-2ax-2a2+a,其中a>0.
(1)设g(x)是f(x)的导函数,讨论g(x)的单调性;
(2)证明:存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
【答案】
(1)
当0<a<![]() 时,g(x)在区间(0,
时,g(x)在区间(0, ![]() ), (
), (![]() ,+
,+![]() )上单调递增, 在区间(
)上单调递增, 在区间(![]() ,
, ![]() )上单调递减;当a≥
)上单调递减;当a≥![]() 时,在区间(0,+
时,在区间(0,+![]() )上单调递增.
)上单调递增.
(2)
详见解析.
【解析】(1)由已知, 函数f(x)的定义域为(0,+![]() ), g(x)=f'(x)=2x-2a-2lnx-2(1+
), g(x)=f'(x)=2x-2a-2lnx-2(1+![]() ), 所以 g'(x)=2-
), 所以 g'(x)=2-![]() +
+![]() =
=![]() , 当0<a<
, 当0<a<![]() 时,g(x)在区间(0,
时,g(x)在区间(0, ![]() ), (
), (![]() ,+
,+![]() )上单调递增, 在区间(
)上单调递增, 在区间(![]() ,
, ![]() )上单调递减;当a≥
)上单调递减;当a≥![]() 时,在区间(0,+
时,在区间(0,+![]() )上单调递增. (2)由f'(x)=2x-2a-2lnx-2(1+
)上单调递增. (2)由f'(x)=2x-2a-2lnx-2(1+![]() )=0, 解得a=
)=0, 解得a=![]() , 令
, 令![]() (x)=-2(x+
(x)=-2(x+![]() )lnx+x2-2(
)lnx+x2-2(![]() )x-2(
)x-2(![]() )2+
)2+![]() , 则
, 则![]() (1)=1>0,
(1)=1>0, ![]() (e)=-
(e)=-![]() -2
-2![]() <0, 故存在x0
<0, 故存在x0![]() (1,e), 使得
(1,e), 使得![]() (x0)=0, 令a0=
(x0)=0, 令a0=![]() , u(x)=x-1-lnx(x≥1), 由u'(x)=1-
, u(x)=x-1-lnx(x≥1), 由u'(x)=1-![]() ≥0知, 函数u(x)在区间(1, +
≥0知, 函数u(x)在区间(1, +![]() )上单调递增。所以0=
)上单调递增。所以0=![]() , 即a
, 即a![]() (0,1), 当a=a0时, 有f'(x0)=0, f(x0)=
(0,1), 当a=a0时, 有f'(x0)=0, f(x0)= ![]() (x0)=0, 由(1)知, 函数f'(x)在区间(1,+
(x0)=0, 由(1)知, 函数f'(x)在区间(1,+![]() )上单调递增., 故当x
)上单调递增., 故当x![]() (1,x0)时, 有f'(x0)<0, 从而f(x)> f(x0)=0, 当x
(1,x0)时, 有f'(x0)<0, 从而f(x)> f(x0)=0, 当x![]() (x0, +
(x0, +![]() )时, 有f'(x0)>0, 从而f(x)> f(x0)=0, 所以, 当x
)时, 有f'(x0)>0, 从而f(x)> f(x0)=0, 所以, 当x![]() (1,+
(1,+![]() )时, f(x)≥0。 综上所述,存在a
)时, f(x)≥0。 综上所述,存在a![]() (0,1),使得f(x)≥0,在区间(1,+
(0,1),使得f(x)≥0,在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解.
)内有唯一解.
本题考查导数的运算、导数在研究函数中的应用、函数的零点等基础知识,考查推理论证能力、运算求解能力、创新意识,考查函数与方程、数形结合、分类与 整合,化归与转化等数学思想.本题作为压轴题,难度系数应在0.3以下.导数与微积分作为大学重要内容,在中学要求学生掌握其基础知识,在高考题中也必有 体现.一般地,只要掌握了课本知识,是完全可以解决第(1)题的,所以对难度最大的最后一个题,任何人都不能完全放弃,这里还有不少的分是志在必得的.解 决函数题需要的一个重要数学思想是数形结合,联系图形大胆猜想. 在本题中,结合待证结论,可以想象出f(x)的大致图象,要使得f(x)≥0在区间(1,+![]() )内恒成立,且f(x)=0在(1,+
)内恒成立,且f(x)=0在(1,+![]() )内有唯一解,则这个解x0应为极小值点,且极小值为0,当x
)内有唯一解,则这个解x0应为极小值点,且极小值为0,当x![]() (1,x0)时,f(x)的图象递减; 当x
(1,x0)时,f(x)的图象递减; 当x![]() (1,+
(1,+![]() )时,f(x)的图象单调递增,顺着这个思想,便可找到解决方法.
)时,f(x)的图象单调递增,顺着这个思想,便可找到解决方法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】如图,在几何体ABCDEF中,四边形ABCD是菱形,BE⊥平面ABCD,DF∥BE,且DF=2BE=2,EF=3. 
(1)证明:平面ACF⊥平面BEFD
(2)若二面角A﹣EF﹣C是二面角,求直线AE与平面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 新课标II)在直角坐标系xoy中,曲线C1:
新课标II)在直角坐标系xoy中,曲线C1:![]() (t为参数,t≠0),其中0
(t为参数,t≠0),其中0![]()
![]()
![]() ,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:![]() =2sin
=2sin![]() ,C3:
,C3:![]() =2
=2![]() cos
cos![]()
(1)(Ⅰ)求C2与C1交点的直角坐标
(2)(Ⅱ)若C2与C1相交于点A,C3与C1相交于点B,求|AB|的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱台![]() 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,![]() ,且
,且![]() 底面
底面![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上.
上.
(1)若是![]() 是
是![]() 的中点,证明:
的中点,证明:![]() ;
;
(2若![]() //平面
//平面![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求四面体
,求四面体![]() 的体积
的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)设数列{an}的前n项和Sn=2an-a1 , 且a1, a2+1, a3成等差数列.
(1)求数列{an}的通项公式;
(2)记数列{![]() }的前n项和Tn , 求Tn。
}的前n项和Tn , 求Tn。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)设数列{an}的前n项和Sn=2an-a1 , 且a1, a2+1, a3成等差数列.
(1)求数列{an}的通项公式;
(2)记数列{![]() }的前n项和Tn , 求得|Tn-1|<
}的前n项和Tn , 求得|Tn-1|<![]() 成立的n的最小值.
成立的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路的山区边界的直线型公路,记两条相互垂直的公路为了l1, l2 , 山区边界曲线为C , 计划修建的公路为l , 如图所示,M , N为C的两个端点,测得点M到l1, l2 的距离分别为5千米和40千米,点N到l1, l2的距离分别为20千米和2.5千米,以l1, l2所在的直线分别为x , y轴,建立平面直角坐标系xOy , 假设曲线C符合函数y=![]() (其中a , b为常数)模型.
(其中a , b为常数)模型.
(1)求a , b的值;
(2)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式f(t),并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 已知点F为抛物线E:
已知点F为抛物线E:![]() 的焦点,点A(2,m)在抛物线E上,且|AF|=3
的焦点,点A(2,m)在抛物线E上,且|AF|=3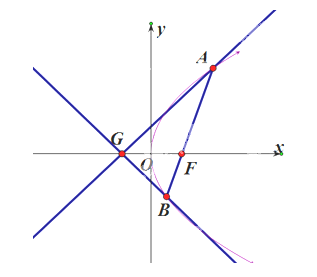 .
.
(1)求抛物线E的方程;
(2)已知点G(-1,0) , 延长AF交抛物线E于点B , 证明:以点F为圆心且与直线GA相切的圆,必与直线GB相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com