
已知函数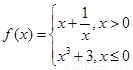 ,则关于
,则关于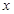 的方程
的方程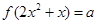 (
(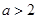 )的解的个数可能为 (写出所有可能的结果).
)的解的个数可能为 (写出所有可能的结果).
4、5、6
【解析】
试题分析:易知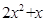 的取值范围为
的取值范围为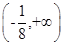 ,设
,设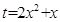 ,则
,则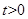 时,
时,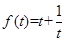 为双钩函数的一支,最小值为2,在t=1时取到;当
为双钩函数的一支,最小值为2,在t=1时取到;当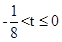 ,f(t)的取值范围为
,f(t)的取值范围为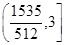 ,并且是单调递增。分别判断各种情况:
,并且是单调递增。分别判断各种情况: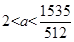 ,则只有当t>0时有根,此时t有两个解,而
,则只有当t>0时有根,此时t有两个解,而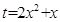 为二次函数,因此x有四个根;当a>3时,同上可知,只有t>0是有根,x有四个解;当
为二次函数,因此x有四个根;当a>3时,同上可知,只有t>0是有根,x有四个解;当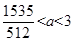 时,此时t>0时有两个解,t<0时有一个解,因此x有六个根;当
时,此时t>0时有两个解,t<0时有一个解,因此x有六个根;当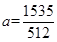 时,同上,此时在t>0时有两个解,而t<0时有一个解,但在t<0处x有唯一解,因此x有五个根。综上,该方程根的个数可能为4、5、6个,其余个数均不可能。
时,同上,此时在t>0时有两个解,而t<0时有一个解,但在t<0处x有唯一解,因此x有五个根。综上,该方程根的个数可能为4、5、6个,其余个数均不可能。
考点:双钩函数;基本不等式;二次函数的性质。函数图像的综合应用。
点评:本题考查函数的单调性,考查函数与方程的联系,做本题的关键是画出图形,根据图形分析出解得各种情况。有一定的难度.


科目:高中数学 来源: 题型:
 给出下列四个命题:
给出下列四个命题:| π |
| 6 |
| 5 |
| 6 |
| OA |
| OB |
| OC |
| ||
|
| 1 |
| 12 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年安徽省六安一中高三(下)第七次月考数学试卷(理科)(解析版) 题型:填空题
 ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com