
【题目】已知函数![]() 在
在![]() 处取得极值
处取得极值![]() ,其中
,其中![]() 为常数.若对任意
为常数.若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】![]() .
.
【解析】试题分析: 函数![]() 在
在![]() 处取得极值
处取得极值![]() ,即
,即![]() ,
, ![]() ,列出方程组可求出a,b的值,代入函数
,列出方程组可求出a,b的值,代入函数![]() 求出解析式,对函数求导判断单调性,求出函数的极小值, 且此极小值也是最小值, 要使
求出解析式,对函数求导判断单调性,求出函数的极小值, 且此极小值也是最小值, 要使![]() 对任意
对任意![]() 恒成立,只需
恒成立,只需![]() 小于等于函数的最小值,代入解出c的取值范围即可.
小于等于函数的最小值,代入解出c的取值范围即可.
试题解析:
由题意知f(1)=b-c=-3-c,因此b=-3.
对f(x)求导,得
f′(x)=4ax3ln x+ax4·![]() +4bx3
+4bx3
=x3(4aln x+a+4b).
由题意知f′(1)=0,得a+4b=0,解得a=12,
从而f′(x)=48x3ln x(x>0).令f′(x)=0,解得x=1.
当0<x<1时,f′(x)<0,此时f(x)为减函数;
当x>1时,f′(x)>0,此时f(x)为增函数.
所以f(x)在x=1处取得极小值f(1)=-3-c,
并且此极小值也是最小值.
所以要使f(x)≥-2c2(x>0)恒成立,只需-3-c≥-2c2即可.
整理得2c2-c-3≥0,解得c≥![]() 或c≤-1.
或c≤-1.
所以c的取值范围为![]() .
.
点睛: 本题考查利用导数判断函数的单调性,求函数的极值和最值以及函数的恒成立问题,属于中档题目.恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解,注意利用数形结合的数学思想方法.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
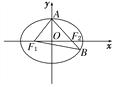
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设{an}是由正数组成的等比数列,公比q=2,且a1a2a3…a30=230 , 那么a3a6a9…a30等于( )
A.210
B.220
C.216
D.215
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
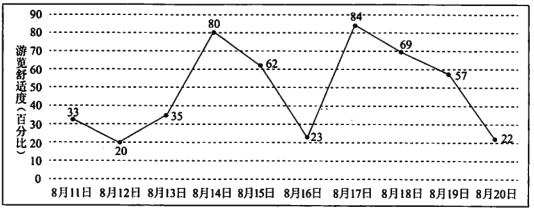
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com