
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项的和.
项的和.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() ,18,
,18,![]() 成等比数列,求正整数
成等比数列,求正整数![]() 的值;
的值;
(3)是否存在![]() ,使得
,使得![]() 为数列
为数列![]() 中的项?若存在,求出所有满足条件的
中的项?若存在,求出所有满足条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() .(2)
.(2)![]() ,
,![]() .(3)
.(3)![]() 或14.
或14.
【解析】试题分析:(1)当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,由
时,由![]()
![]()
![]()
![]() 列
列![]() 是首项为2,公差为1的等差数列
是首项为2,公差为1的等差数列![]()
![]() .
.
(2)建立方程组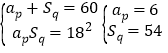 ,或
,或![]() .当
.当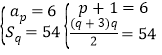
![]()
![]() ,当
,当![]()
![]() 无正整数解,综上
无正整数解,综上![]() ,
,![]() .
.
(3)假设存在正整数![]() ,使得
,使得![]() ,
,![]()
![]()
![]()
![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() ,
,![]() (舍去)
(舍去)![]()
![]() 或14.
或14.
试题解析:
(1)因为![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,
由![]()
![]() 和
和![]() ,
,
两式相除可得,![]() ,即
,即![]()
所以,数列![]() 是首项为2,公差为1的等差数列.
是首项为2,公差为1的等差数列.
于是,![]() .
.
(2)因为![]() ,30,
,30,![]() 成等差数列,
成等差数列,![]() ,18,
,18,![]() 成等比数列,
成等比数列,
所以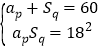 ,于是
,于是![]() ,或
,或![]() .
.
当![]() 时,
时,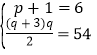 ,解得
,解得![]() ,
,
当![]() 时,
时,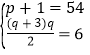 ,无正整数解,
,无正整数解,
所以![]() ,
,![]() .
.
(3)假设存在满足条件的正整数![]() ,使得
,使得![]() ,
,
则![]() ,
,
平方并化简得,![]() ,
,
则![]() ,
,
所以![]() ,或
,或![]() ,或
,或![]() ,
,
解得:![]() ,
,![]() 或
或![]() ,
,![]() ,或
,或![]() ,
,![]() (舍去),
(舍去),
综上所述,![]() 或14.
或14.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,某街道居委会拟在![]() 地段的居民楼正南方向的空白地段
地段的居民楼正南方向的空白地段![]() 上建一个活动中心,其中
上建一个活动中心,其中![]() 米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形
米.活动中心东西走向,与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形![]() ,上部分是以
,上部分是以![]() 为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长
为直径的半圆. 为了保证居民楼住户的采光要求,活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长![]() 不超过
不超过![]() 米,其中该太阳光线与水平线的夹角
米,其中该太阳光线与水平线的夹角![]() 满足
满足![]() .
.

(1)若设计![]() 米,
米,![]() 米,问能否保证上述采光要求?
米,问能否保证上述采光要求?
(2)在保证上述采光要求的前提下,如何设计![]() 与
与![]() 的长度,可使得活动中心的截面面积最大?(注:计算中
的长度,可使得活动中心的截面面积最大?(注:计算中![]() 取3)
取3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记1分,海选不合格记0分.假设甲、乙、丙海选合格的概率分别为![]() ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com