
【题目】设椭圆E:![]() +
+![]() =1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为
=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为![]() ,三角形ABF2的周长为4
,三角形ABF2的周长为4![]() .
.
(1)求椭圆E的方程;
(2)设不经过椭圆的中心而平行于弦AB的直线交椭圆E于点C,D,设弦AB,CD的中点分别为M,N,证明:O,M,N三点共线.
【答案】(1)![]() +
+![]() =1;(2)证明见解析
=1;(2)证明见解析
【解析】
(1)根据椭圆的定义由三角形ABF2的周长求出a,代入离心率求出c,再求出b,即可求得椭圆的方程;(2)直线斜率不存在时由椭圆的对称性即可证明;直线斜率存在时,设A(x1,y1),B(x2,y2),M(x0,y0),A,B 点的坐标代入方程,两式相减利用中点坐标公式变形可求出直线OM的斜率,同理可求出ON的斜率,两斜率相等即可得证.
(1)![]() ,
,![]() a=
a=![]() ,
,
又e=![]() ,∴c=
,∴c=![]() ,b=
,b=![]() ,
,
∴椭圆E的方程为![]() +
+![]() =1.
=1.
(2)当直线AB,CD的斜率不存在时,由椭圆的对称性知,中点M,N在x轴上,O,M,N三点共线;
当直线AB,CD的斜率存在时,设其斜率为k(k≠0),
且设A(x1,y1),B(x2,y2),M(x0,y0),
则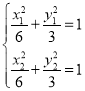 ,两式相减,得
,两式相减,得![]() =-
=-![]() ,
,
又![]() ,所以
,所以![]() ·
·![]() =-
=-![]() ,
,
则![]() -
-![]()
![]() -
-![]() .
.
同理可得![]() -
-![]() ,
,![]() ,∴O,M,N三点共线.
,∴O,M,N三点共线.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“![]() ”表示一个阳爻,“
”表示一个阳爻,“![]() ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )
”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 图象在
图象在![]() 处的切线方程;
处的切线方程;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() 存在极大值和极小值,且极大值小于极小值,求
存在极大值和极小值,且极大值小于极小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史上有不少数学家都对圆周率作过研究,第一个用科学方法寻求圆周率数值的人是阿基米德,他用圆内接和外切正多边形的周长确定圆周长的上下界,开创了圆周率计算的几何方法,而中国数学家刘徽只用圆内接正多边形就求得![]() 的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种
的近似值,他的方法被后人称为割圆术.近代无穷乘积式、无穷连分数、无穷级数等各种![]() 值的表达式纷纷出现,使得
值的表达式纷纷出现,使得![]() 值的计算精度也迅速增加.华理斯在1655年求出一个公式:
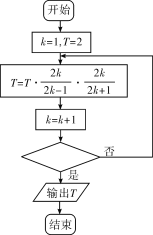
值的计算精度也迅速增加.华理斯在1655年求出一个公式:![]() ,根据该公式绘制出了估计圆周率
,根据该公式绘制出了估计圆周率![]() 的近似值的程序框图,如下图所示,执行该程序框图,已知输出的
的近似值的程序框图,如下图所示,执行该程序框图,已知输出的![]() ,若判断框内填入的条件为
,若判断框内填入的条件为![]() ,则正整数
,则正整数![]() 的最小值是
的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,∠ABC=60°,AA1![]() AB,M,N分别为AB,AA1的中点.
AB,M,N分别为AB,AA1的中点.
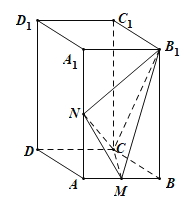
(1)求证:平面B1NC⊥平面CMN;
(2)若AB=2,求点N到平面B1MC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为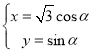 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() ,点
,点![]() 为曲线
为曲线![]() 上的动点,求线段
上的动点,求线段![]() 的中点
的中点![]() 到直线
到直线![]() 的距离的最大值.并求此时点
的距离的最大值.并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)如果对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)讨论函数![]() 的零点个数.
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com