
【题目】已知数列![]() ,
,![]() 满足
满足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,则数列
,则数列![]() 中第几项最小?请说明理由;
中第几项最小?请说明理由;
(3)若![]() (n=1,2,3,…),求证:“数列
(n=1,2,3,…),求证:“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
【答案】(1)![]() (2)第8项最小,理由见解析(3)证明见解析
(2)第8项最小,理由见解析(3)证明见解析
【解析】
(1)由![]() 可判断
可判断![]() 是等差数列,则
是等差数列,则![]()
![]() ,进而利用等差数列性质求解即可;
,进而利用等差数列性质求解即可;
(2)法一:利用数列的增减性进行判断即可;
法二:求出![]() 的通项公式,利用均值不等式求最值,即可得到取等条件,进而求解;
的通项公式,利用均值不等式求最值,即可得到取等条件,进而求解;
(3)若数列![]() 为等差数列,设其公差为
为等差数列,设其公差为![]() ,说明数列
,说明数列![]() 为等差数列,由
为等差数列,由![]() (
(![]() …)推出
…)推出![]() (
(![]() …);若数列
…);若数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…),设公差为
(n=1,2,3,…),设公差为![]() ,转化推出
,转化推出![]() (
(![]() …),说明数列
…),说明数列![]() 为等差数列,结论得证
为等差数列,结论得证
(1)由![]() ,可得
,可得![]() ,故
,故![]() 是等差数列,
是等差数列,
所以![]()
![]()
(2)![]()
![]()
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
当![]() 时,则
时,则![]() ,解得
,解得![]() ,
,
故有![]() ,
,
所以数列![]() 中
中![]() 最小,即第8项最小
最小,即第8项最小
法二:由![]() ,
,
可知![]()
![]()
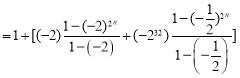
![]()
![]() (当且仅当
(当且仅当![]() ,即
,即![]() 时取等号)
时取等号)
所以数列![]() 中的第8项最小
中的第8项最小
(3)证明:若数列![]() 为等差数列,设其公差为
为等差数列,设其公差为![]() ,
,
则![]() 为常数,
为常数,
所以数列![]() 为等差数列,
为等差数列,
由![]() (
(![]() …),
…),
则![]() ,故
,故![]() (
(![]() …)成立,故必要性成立;
…)成立,故必要性成立;
若数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…),设
(n=1,2,3,…),设![]() 的公差为
的公差为![]() ,
,
则![]() (n=1,2,3,…),
(n=1,2,3,…),
又![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,故
,故![]() ,
,
所以![]()
![]() ,故有
,故有![]() ,所以
,所以![]() 为常数,
为常数,
故数列![]() 为等差数列,故充分性成立,
为等差数列,故充分性成立,
综上可得,“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”
(n=1,2,3,…)”


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(![]() )求数列
)求数列![]() 的通项公式;
的通项公式;
(![]() )若数列
)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 平面
平面![]() 为正三角形, 侧面
为正三角形, 侧面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 的中点.
的中点.
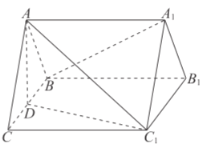
(1)求证![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是反映空气质量状况的指数,
是反映空气质量状况的指数,![]() 指数值越小,表明空气质量越好,其对应关系如表:
指数值越小,表明空气质量越好,其对应关系如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市10月1日—20日![]() 指数变化趋势:
指数变化趋势:
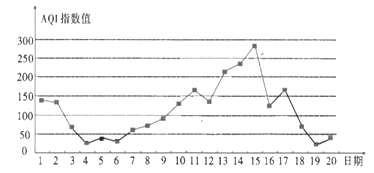
下列叙述正确的是( )
A.该市10月的前半个月的空气质量越来越好
B.这20天中的中度污染及以上的天数占![]()
C.这20天中![]() 指数值的中位数略高于100
指数值的中位数略高于100
D.总体来说,该市10月上旬的空气质量比中旬的空气质量差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一幢高楼上安放了一块高约10 米的 LED 广告屏,一测量爱好者在与高楼底部同一水平线上的 C 处测得广告屏顶端A 处的仰角为 31.80°,再向大楼前进 20 米到 D 处,测得广告屏顶端 A 处的仰角为 37.38°(人的高度忽略不计).
(1)求大楼的高度(从地面到广告屏顶端)(精确到 1 米);
(2)若大楼的前方是一片公园空地,空地上可以安放一些长椅,为使坐在其中一个长椅上观看广告屏最清晰(长 椅的高度忽略不计),长椅需安置在距大楼底部 E 处多远?已知视角 ∠AMB( M 为观测者的位置, B 为广告屏 底部)越大,观看得越清晰.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com