
【题目】(1)掷两枚质地均匀的骰子,计算点数和为7的概率;
(2)利用随机模拟的方法,试验120次,计算出现点数和为7的频率;
(3)所得频率与概率相差大吗?为什么会有这种差异?
【答案】(1)![]() (2)答案见解析 (3)答案见解析
(2)答案见解析 (3)答案见解析
【解析】
(1)写出基本事件,根据概率的计算公式,即可求得答案;
(2)利用计算机生成随机数表,即可计算出现点数和为7的频率;
(3)分析(1)和(2)所得数据,即可求得答案.
(1)抛掷两枚骰子,向上的点数有
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6);
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6);
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6);
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6);
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6);
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6).
共36种情况,其中点数和为7的有6种情况,
![]() 概率
概率![]() .
.
(2)
63 | 51 | 35 | 66 | 42 |
54 | 66 | 42 | 64 | 22 |
46 | 36 | 42 | 26 | 55 |
53 | 51 | 12 | 32 | 24 |
62 | 52 | 32 | 12 | 63 |
61 | 31 | 12 | 22 | 64 |
64 | 12 | 51 | 23 | 52 |
46 | 25 | 32 | 65 | 41 |
31 | 31 | 15 | 43 | 13 |
52 | 42 | 15 | 52 | 26 |
22 | 61 | 65 | 42 | 25 |
14 | 42 | 11 | 25 | 42 |
26 | 62 | 36 | 41 | 62 |
34 | 31 | 31 | 16 | 24 |
64 | 34 | 22 | 45 | 62 |
54 | 16 | 34 | 22 | 64 |
12 | 23 | 54 | 41 | 54 |
52 | 21 | 45 | 35 | 66 |
13 | 65 | 11 | 14 | 41 |
51 | 54 | 32 | 36 | 44 |
52 | 42 | 15 | 52 | 26 |
22 | 61 | 65 | 42 | 25 |
53 | 52 | 16 | 32 | 24 |
62 | 52 | 32 | 12 | 63 |
规定每个表格中的第一个数字代表第一个骰子出现的数字,
第二个数字代表第二个骰子出现的数字
从表格中可以查出点数和为7等于23个数据
![]() 点数和为7的频率为:
点数和为7的频率为:![]()
(3)由(1)中点数和为7的概率为![]()
由(2)点数和为7的频率为:![]()
一般来说频率与概率有一定的差距,因为模拟的次数不多,不一定能反映真实情况.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】定义:若对定义域内任意x,都有![]() (a为正常数),则称函数
(a为正常数),则称函数![]() 为“a距”增函数.
为“a距”增函数.
(1)若![]() ,
,![]() (0,
(0,![]() ),试判断
),试判断![]() 是否为“1距”增函数,并说明理由;
是否为“1距”增函数,并说明理由;
(2)若![]() ,
,![]() R是“a距”增函数,求a的取值范围;
R是“a距”增函数,求a的取值范围;
(3)若![]() ,
,![]() (﹣1,
(﹣1,![]() ),其中k
),其中k![]() R,且为“2距”增函数,求
R,且为“2距”增函数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,离心率为
,离心率为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任一点,且
上任一点,且![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 过椭圆的左焦点
过椭圆的左焦点![]() ,与椭圆交于
,与椭圆交于![]() 两点,且
两点,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
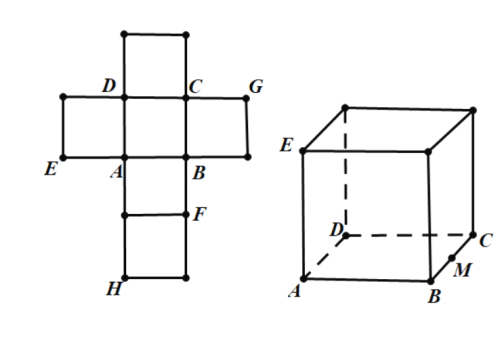
(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(Ⅲ)证明:直线DF![]() 平面BEG
平面BEG
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面取球的试验,并模拟100次,估计“取出的球是白球”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法正确的是( )
①若![]() 和
和![]() 都是定义在
都是定义在![]() 上的函数,则“
上的函数,则“![]() 与
与![]() 同是奇函数”是“
同是奇函数”是“![]() 是偶函数”的充要条件
是偶函数”的充要条件
②命题 “![]() ”的否定是“
”的否定是“![]()
![]() ≤0”
≤0”
③命题“若x=2,则![]() ”的逆命题是“若
”的逆命题是“若![]() ,则x=2”
,则x=2”
④命题![]() :在
:在![]() 中,若
中,若![]() ,则
,则![]() ;
;
命题![]() :
:![]() 在第一象限是增函数;
在第一象限是增函数;
则![]() 为真命题
为真命题
A. ①②③④ B. ①③ C. ③④ D. ③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)当![]() 时,是否存在正实数
时,是否存在正实数![]() ,当
,当![]() (
(![]() 是自然对数底数)时,函数
是自然对数底数)时,函数![]() 的最小值是3,若存在,求出
的最小值是3,若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com