
【题目】已知函数![]() (其中
(其中![]() 是实数).
是实数).
(1)求![]() 的单调区间;
的单调区间;
(2)若设![]() ,且
,且![]() 有两个极值点
有两个极值点![]() ,
,![]() (
(![]() ),求
),求![]() 取值范围.(其中
取值范围.(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,当
,无单调递减区间,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)求出![]() 的定义域为
的定义域为![]() ,
,![]() ,由此利用导数性质和分类讨论思想能求出
,由此利用导数性质和分类讨论思想能求出![]() 的单调区间;(2)推导出
的单调区间;(2)推导出![]() ,令
,令![]() ,则
,则![]() 恒成立,由此能求出
恒成立,由此能求出![]() 的取值范围.
的取值范围.
试题解析:(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() ,
,![]() ,对称轴
,对称轴![]() ,
,![]() ,
,
(1)当![]() ,即
,即![]() 时,
时,![]()
于是,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
(2)当![]() ,即
,即![]() 或
或![]() 时,①若
时,①若![]() ,则
,则![]() 恒成立
恒成立
于是,![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间.②若
,无减区间.②若![]()
令![]() ,得
,得![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
于是,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .综上所述:
.综上所述:
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由(1)知,若![]() 有两个极值点,则
有两个极值点,则![]() ,且
,且![]() ,
,![]() ,
,
![]()
又![]() ,
,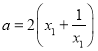 ,
,![]() ,
,![]() ,又
,又![]() ,解得,
,解得,![]() 于是,
于是,![]()
![]()
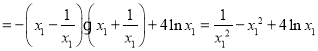
令![]() (
(![]() ),则
),则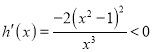 恒成立,
恒成立,![]() 在
在![]() 单调递减,
单调递减,![]() ,即
,即![]() ,故
,故![]() 的取值范围为
的取值范围为![]()


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有Ⅳ人参加,现将所有参加者按年龄情况分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等七组,其频率分布直方图如图所示,已知
等七组,其频率分布直方图如图所示,已知![]() 这组的参加者是6人.
这组的参加者是6人.
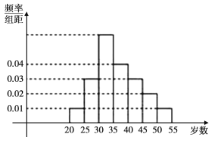
(1)已知![]() 和
和![]() 这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中恰有1名数学老师的概率;
(2)组织者从![]() 这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为
这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为![]() ,求
,求![]() 的分布列和均值.
的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 上有一动点
上有一动点![]() ,过点
,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,动点
轴,动点![]() 在
在![]() 上,且满足
上,且满足![]() (
(![]() 为坐标原点),记点
为坐标原点),记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)已知定点![]() ,
,![]() ,
,![]() 为曲线
为曲线![]() 上一点,直线
上一点,直线![]() 交曲线
交曲线![]() 于另一点
于另一点![]() ,且点
,且点![]() 在线段
在线段![]() 上,直线
上,直线![]() 交曲线
交曲线![]() 于另一点
于另一点![]() ,求
,求![]() 的内切圆半径
的内切圆半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,定义
,定义![]() ,其中
,其中![]() 为坐标原点,对于下列结论:
为坐标原点,对于下列结论:
![]() 符合
符合![]() 的点
的点![]() 的轨迹围成的图形面积为8;
的轨迹围成的图形面积为8;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则
上任意一点,则![]() ;
;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则使得“
上任意一点,则使得“![]() 最小的点有无数个”的充要条件是
最小的点有无数个”的充要条件是![]() ;
;
![]() 设点
设点![]() 是椭圆
是椭圆![]() 上任意一点,则
上任意一点,则![]() .
.
其中正确的结论序号为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第三季)亮点颇多,在“人生自有诗意”的主题下,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场,且《蜀道难》排在《游子吟》的前面,《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后,则后六场的排法有__________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一年级某个班分成7个小组,利用假期参加社会公益服务活动![]() 每个小组必须全员参加
每个小组必须全员参加![]() ,参加活动的次数记录如下:
,参加活动的次数记录如下:
组别 |
|
|
|
|
|
|
|
参加活动次数 | 3 | 2 | 4 | 3 | 3 | 4 | 2 |
![]() Ⅰ
Ⅰ![]() 求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
![]() Ⅱ
Ⅱ![]() 从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
![]() Ⅲ
Ⅲ![]() 至
至![]() 小组每组有4名同学,
小组每组有4名同学,![]() 小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为
小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为![]() ,写出
,写出![]() 与v的大小关系
与v的大小关系![]() 结论不要求证明
结论不要求证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4 坐标系与参数方程选讲
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 极坐标方程为
极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的参数方程;
的参数方程;
(2)当![]() 时,
时,![]() 为曲线
为曲线![]() 上动点,求点
上动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com