
【题目】一种电子计时器显示时间的方式如图所示,每一个数字都在固定的全等矩形“显示池”中显示,且每个数字都由若干个全等的深色区域“ ![]() ”组成.已知在一个显示数字8的显示池中随机取一点
”组成.已知在一个显示数字8的显示池中随机取一点![]() ,点
,点![]() 落在深色区域内的概率为
落在深色区域内的概率为![]() .若在一个显示数字0的显示池中随机取一点
.若在一个显示数字0的显示池中随机取一点![]() ,则点
,则点![]() 落在深色区域的概率为( )
落在深色区域的概率为( )
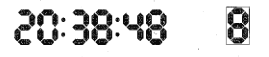
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”,则该课程考核“合格”,若甲、乙、丙三人在理论考核中合格的概率分别为0.9,0.8,0.7,在实验考核中合格的概率分别为0.8,0.7,0.9,所有考核是否合格相互之间没有影响.
(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(2)求这三个人该课程考核都合格的概率(结果保留三位小数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,以x轴非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的参数方程为![]() (θ为参数),直线l的极坐标方程为ρcos
(θ为参数),直线l的极坐标方程为ρcos![]() =2
=2![]() .
.
(1)写出曲线C的普通方程和直线l的直角坐标方程;
(2)求曲线C上的点到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在浙江省和青海省各取面积大小一样的A,B两块区域,分别调查人均可支配收入.获得数据显示,浙江省的A区域的人均可支配收入为35537元,青海省的B区域的人均可支配收入为24542元.
(1)能否得到这两块区域的人均可支配收入为![]() (元)?
(元)?
(2)若“A区域为70万人,B区域为30万人”,请问这两块区域的人均可支配收入为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{![]() }的前
}的前![]() 项和为Sn,且Sn=n(n+1)(n∈N*).
项和为Sn,且Sn=n(n+1)(n∈N*).
(1)若数列![]() 满足:
满足:![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列{
,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
(3)![]()
![]() ,(n为正整数),问是否存在非零整数
,(n为正整数),问是否存在非零整数![]() ,使得对任意正整数n,都有
,使得对任意正整数n,都有![]() 若存在,求
若存在,求![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励市民节约用电,某市实行“阶梯式”电价,将每户居民的月用电量分为二档,月用电量不超过200度的部分按0.5元/度收费,超过200度的部分按0.8元/度收费.某小区共有居民1000户,为了解居民的用电情况,通过抽样,获得了今年7月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图.

(1)求![]() 的值;
的值;
(2)试估计该小区今年7月份用电量用不超过260元的户数;
(3)估计7月份该市居民用户的平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com