
【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分,每项评分最低分0分,最高分100分,每个景点总分为这五项得分之和,根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下:
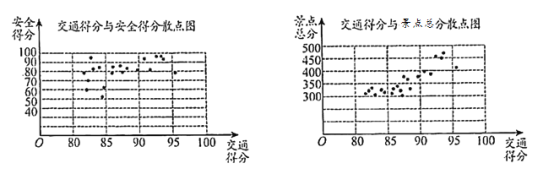
请根据图中所提供的信息,完成下列问题:
(I)若从交通得分前6名的景点中任取2个,求其安全得分都大于90分的概率;
(II)若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)记该市26个景点的交通平均得分为![]() 安全平均得分为
安全平均得分为![]() ,写出
,写出![]() 和
和![]() 的大小关系?(只写出结果)
的大小关系?(只写出结果)
【答案】(I)![]() ;(II)分布列见解析,期望为
;(II)分布列见解析,期望为![]() ;(III)
;(III)![]()
【解析】
(I)根据古典概型概率计算公式,计算出所求概率.
(II)利用超几何分布的知识求出分布列和数学期望.
(III)根据两种得分的数据离散程度进行判断.
(I)由图可知,交通得分前![]() 名的景点中,安全得分大于
名的景点中,安全得分大于![]() 分的景点有
分的景点有![]() 个,所以从交通得分前
个,所以从交通得分前![]() 名的景点中任取
名的景点中任取![]() 个,求其安全得分都大于
个,求其安全得分都大于![]() 分的概率为
分的概率为![]() .
.
(II)结合两个图可知,景点总分排名前![]() 的的景点中,安全得分不大于
的的景点中,安全得分不大于![]() 分的景点有
分的景点有![]() 个,所以
个,所以![]() 的可能取值为
的可能取值为![]() .
.
![]() .
.
所以![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
所以![]() .
.
(III)由图可知,![]() 个景点中,交通得分全部在
个景点中,交通得分全部在![]() 分以上,主要集中在
分以上,主要集中在![]() 分附近,安全得分主要集中在
分附近,安全得分主要集中在![]() 分附近,且
分附近,且![]() 分一下的景点接近一半,故
分一下的景点接近一半,故 ![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D、E分别是AC、BC的中点,F在SE上,且SF=2FE.
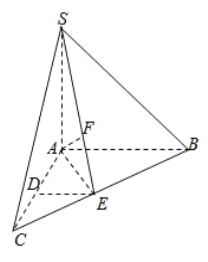
(1)求证:平面SBC⊥平面SAE
(2)若G为DE中点,求二面角G﹣AF﹣E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,曲线
轴的正半轴重合,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是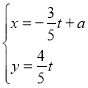 (
(![]() 为参数).
为参数).
(1)若![]() ,
,![]() 是圆
是圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离
的距离![]() 的最小值和最大值;
的最小值和最大值;
(2)直线![]() 与
与![]() 关于原点对称,且直线
关于原点对称,且直线![]() 截曲线
截曲线![]() 的弦长等于
的弦长等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x-1+![]() (a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(a∈R,e为自然对数的底数).且曲线y=f(x)在点(1,f(1))处的切线平行于x轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
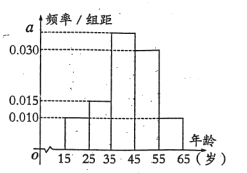
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,设第2组抽到![]() 人,求随机变量
人,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家正积极推行垃圾分类工作,教育部办公厅等六部门也发布了《关于在学校推进生活垃圾分类管理工作的通知》.《通知》指出,到2020年底,各学校生活垃圾分类知识普及率要达到100%某市教育主管部门据此做了“哪些活动最能促进学生进行垃圾分类”的问卷调查(每个受访者只能在问卷的4个活动中选择一个)如图是调查结果的统计图,以下结论正确的是( )
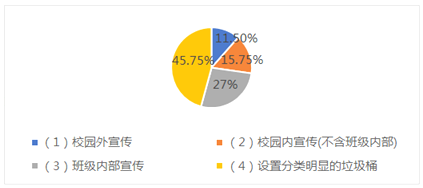
A.回答该问卷的受访者中,选择的(2)和(3)人数总和比选择(4)的人数多
B.回该问卷的受访者中,选择“校园外宣传”的人数不是最少的
C.回答该问卷的受访者中,选择(4)的人数比选择(2)的人数可能多30人
D.回答该问卷的总人数不可能是1000人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体A-BCD中,已知平面![]() 平面BCD,
平面BCD,![]() 为正三角形,
为正三角形,![]() 为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
为等腰直角三角形,其中C为直角顶点,E,F分别为校AC,AD的中点.
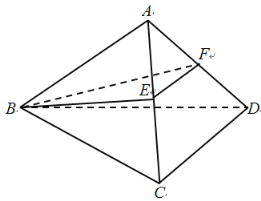
(1)求证:![]() 平面BEF;
平面BEF;
(2)求证:![]() 平面ACD.
平面ACD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
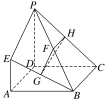
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com