
【题目】在△ABC中,已知角A,B,C所对的边分别为a,b,c,且tanB=2,tanC=3.
(1)求角A的大小;
(2)若c=3,求b的长.
【答案】
(1)解:因为:tanB=2,tanC=3,tan(B+C)= ![]() =
= ![]() =﹣1,
=﹣1,
因为:A=180°﹣B﹣C,
所以:tanA=tan(180°﹣(B+C))=﹣tan(B+C)=1
因为:A∈(0,π),
所以:A= ![]()
(2)解:因为:c=3,tanB=2,tanC=3.
所以:sinB= ![]() ,sinC=
,sinC= ![]() ,
,
所以由正弦定理可得:b= ![]() =
= ![]() =2
=2 ![]()
【解析】(1)利用两角和的正切函数公式表示出tan(B+C),把tanB和tanC的值代入即可求出tan(B+C)的值,根据三角形的内角和定理及诱导公式得到tanA等于﹣tan(B+C),进而得到tanA的值,结合A的范围即可得解;(2)由已知利用同角三角函数基本关系式可求sinB,sinC的值,进而利用正弦定理即可得解b的值.
【考点精析】通过灵活运用两角和与差的正切公式,掌握两角和与差的正切公式:![]() 即可以解答此题.
即可以解答此题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
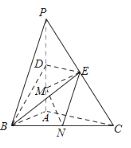
(1)求证:MN∥平面BDE;
(2)求二面角C-EM-N的正弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={x|3+2x﹣x2>0},N={x|x>a},若MN,则实数a的取值范围是( )
A.[3,+∞)
B.(3,+∞)
C.(﹣∞,﹣1]
D.(﹣∞,﹣1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生期末考试数学成绩和总分年级排名如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 |
数学 | 115 | 112 | 93 | 125 | 145 |
年级排名 | 250 | 300 | 450 | 70 | 10 |
(1)通过大量事实证明发现,一个学生的数学成绩和总分年级排名具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示年级排名,求
表示年级排名,求![]() 与
与![]() 的回归方程;(其中
的回归方程;(其中![]() 都取整数)
都取整数)
(2)若在本次考试中,预计数学分数为120分的学生年级排名大概是多少?
参考数据和公式:![]() ,其中
,其中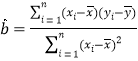 ,
,![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1= ![]() ,an+1=
,an+1= ![]() an﹣
an﹣ ![]() ,n∈N* , 设Sn为{an}的前n项和.
,n∈N* , 设Sn为{an}的前n项和.
(1)求证:数列{3nan}是等差数列;
(2)求Sn;
(3)是否存在正整数p,q,r(p<q<r),使Sp , Sq , Sr成等差数列?若存在,求出p,q,r的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点. 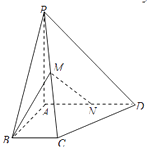
(1)求异面直线AP,BM所成角的余弦值;
(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:

(1)求回归直线方程![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是5元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
参考数据如下:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com