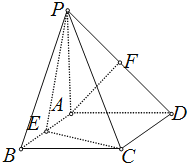
【题目】如图，四棱锥
的底面是正方形，
，
，
，点
分别为棱
的中点.
（1）求证：
∥平面
；
（2）求三棱锥
的体积.
【答案】（1）见解析（2）
【解析】
（1）欲证AF∥平面PCE，根据直线与平面平行的判定定理可知只需证AF与平面PCE内一直线平行，取PC的中点G，连接FG、EG，AF∥EG又EG平面PCE，AF平面PCE，满足定理条件；
（2）三棱锥C﹣BEP的体积可转化成三棱锥P﹣BCE的体积，而PA⊥底面ABCD，从而PA即为三棱锥P﹣BCE的高，根据三棱锥的体积公式进行求解即可．
证明：（1）取PC的中点G，连接FG、EG
∴FG为△CDP的中位线
∴FG
CD
∵四边形ABCD为矩形，E为AB的中点
∴AECD
∴FG
AE
∴四边形AEGF是平行四边形.
∴AF∥EG又EG平面PCE，AF平面PCE
∴AF∥平面PCE.
（2）PA⊥底面ABCD ，在Rt△BCE中，BE=1，BC=2，
∴三棱锥C﹣BEP的体积
VC﹣BEP=VP﹣BCE=
=
.
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案科目：高中数学 来源： 题型：
【题目】如图：某污水处理厂要在一个矩形污水处理池（ABCD）的池底水平铺设污水净化管道（Rt△FHE，H是直角顶点）来处理污水，管道越长，污水净化效果越好．设计要求管道的接口H是AB的中点，E，F分别落在线段BC，AD上．已知AB=20米，AD=10 
米，记∠BHE=θ． 
（1）试将污水净化管道的长度L表示为θ的函数，并写出定义域；
（2）问：当θ取何值时，污水净化效果最好？并求出此时管道的长度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲袋中有1只黑球，3只红球；乙袋中有2只黑球，1只红球.
(1)从甲袋中任取两球，求取出的两球颜色不相同的概率；
(2)从甲，乙两袋中各取一球，求取出的两球颜色相同的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的定义域为
，对任意实数
，都有
．
（1）求
的值并判断函数的奇偶性；
（2）已知函数
，
①验证函数
是否满足题干中的条件，即验证对任意实数，
是否成立；
②若函数
，其中
，讨论函数
的零点个数情况．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=（a+2cos2x）cos（2x+θ）为奇函数，且f（ 
）=0，其中a∈R，θ∈（0，π）．
（1）求a，θ的值；
（2）若f（ 
）=﹣ 
，α∈（ 
，π），求sin（α+ 
）的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若圆C的半径为1，圆心在第一象限，且与直线4x﹣3y=0和x轴都相切，则该圆的标准方程是（ ）
A.（x﹣2）2+（y﹣1）2=1
B.（x﹣2）2+（y+1）2=1
C.（x+2）2+（y﹣1）2=1
D.（x﹣3）2+（y﹣1）2=1
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆C：x2+y2+2x﹣4y+3=0．
（1）若圆C的切线在x轴和y轴上的截距相等，求此切线的方程；
（2）从圆C外一点P（x1 ， y1）向该圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使得|PM|取得最小值的点P的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出以下四个命题：
①如果一条直线和一个平面平行，经过这条直线的一个平面和这个平面相交，那么这条直线和交线平行，
②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面，
③如果两条直线都平行于一个平面，那么这两条直线互相平行，
④如果一个平面经过另一个平面的一条垂线，那么些两个平面互相垂直．
其中真命题的个数是（ ）．
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
