
| A、方程x2+ax+b=0没有实根 |
| B、方程x2+ax+b=0至多有一个实根 |
| C、方程x2+ax+b=0至多有两个实根 |
| D、方程x2+ax+b=0恰好有两个实根 |
科目:高中数学 来源: 题型:
|
| 5 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、
| ||
| D、0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||
| B、ln(x2+1)>ln(y2+1) | ||||
| C、sinx>siny | ||||
| D、x3>y3 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三二诊模拟理科数学试卷(解析版) 题型:解答题
等比数列 中,已知
中,已知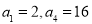 .
.
(1)求数列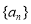 的通项公式;
的通项公式;
(2)若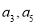 分别为等差数列
分别为等差数列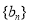 的第3项和第5项,试求数列
的第3项和第5项,试求数列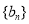 的通项公式及前
的通项公式及前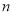 项和
项和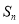 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟理科数学试卷(解析版) 题型:填空题
形如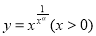 的函数称为“幂指型函数”,它的求导过程可概括成:取对数——两边对
的函数称为“幂指型函数”,它的求导过程可概括成:取对数——两边对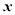 求导——代入还原;例如:
求导——代入还原;例如: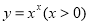 ,取对数
,取对数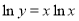 ,对
,对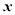 求导
求导 ,代入还原
,代入还原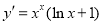 ;给出下列命题:
;给出下列命题:
①当 时,函数
时,函数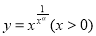 的导函数是
的导函数是 ;②当
;②当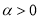 时,函数
时,函数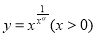 在
在 上单增,在
上单增,在 上单减;③当
上单减;③当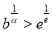 时,方程
时,方程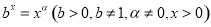 有根;④当
有根;④当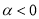 时,若方程
时,若方程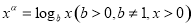 有两根,则
有两根,则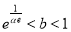 ;
;
其中正确的命题是
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三三诊模拟文科数学试卷(解析版) 题型:解答题
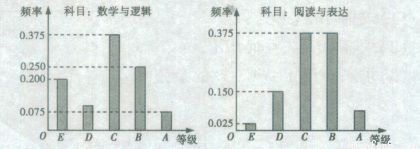
某中学的数学测试中设置了“数学与逻辑”和“阅读与表达”两个内容,成绩分为A、B、C、D、E五个等级。某班考生两科的考试成绩的数据统计如图所示,其中“数学与逻辑”科目的成绩等级为B的考生有10人
(1)求该班考生中“阅读与表达”科目中成绩等级为A的人数;
(2)若等级A、B、C、D、E分别对应5分、4分、3分、2分、1分,该考场中有2人10分,3人9分,从这5人中随机抽取2人,求2人成绩之和为19分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com