
【题目】已知:cos(α+ ![]() )=
)= ![]() ,
, ![]() <α<
<α< ![]() ,求cos(2α+
,求cos(2α+ ![]() ).
).
【答案】解:∵cos(α+ ![]() )=
)= ![]() ,
, ![]() <α<
<α< ![]() ,∴α+
,∴α+ ![]() ∈(
∈( ![]() ,
, ![]() ),sin(α+
),sin(α+ ![]() )=﹣
)=﹣ ![]() ,
,
∴sinα=sin[(α+ ![]() )﹣
)﹣ ![]() ]=sin(α+
]=sin(α+ ![]() )cos
)cos ![]() ﹣cos(α+
﹣cos(α+ ![]() )sin
)sin ![]()
=﹣ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() ,
,
cosα=cos[(α+ ![]() )﹣
)﹣ ![]() ]=cos(α+
]=cos(α+ ![]() )cos
)cos ![]() +sin(α+
+sin(α+ ![]() )sin
)sin ![]()
= ![]() +(﹣
+(﹣ ![]() )
) ![]() =﹣
=﹣ ![]() ,
,
∴sin2α=2sinαcosα= ![]() ,cos2α=2cos2α﹣1=﹣
,cos2α=2cos2α﹣1=﹣ ![]() ,
,
∴cos(2α+ ![]() )=cos2αcos
)=cos2αcos ![]() ﹣sin2αsin
﹣sin2αsin ![]() =﹣
=﹣ ![]()
![]() ﹣
﹣ ![]()
![]() =﹣
=﹣ ![]()
【解析】由条件利用同角三角函数的基本关系求得sin(α+ ![]() )的值,利用两角和差的三角公式求得sinα 和cosα的值,利用二倍角公式求得sin2α和cos2α的值,从而求得cos(2α+
)的值,利用两角和差的三角公式求得sinα 和cosα的值,利用二倍角公式求得sin2α和cos2α的值,从而求得cos(2α+ ![]() )的值.
)的值.
【考点精析】解答此题的关键在于理解二倍角的余弦公式的相关知识,掌握二倍角的余弦公式:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x+ ![]() )+1,△ABC中,角A、B、C的对边分别是a、b、c.
)+1,△ABC中,角A、B、C的对边分别是a、b、c.
(1)若角A、B、C成等差数列,求f(B)的值;
(2)若f( ![]() ﹣
﹣ ![]() )=
)= ![]() ,边a、b、c成等比数列,△ABC的面积S=
,边a、b、c成等比数列,△ABC的面积S= ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足2a1+a3=3a2 , 且a3+2是a2 , a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=an+log2 ![]() ,Sn=b1+b2+…bn , 求使 Sn﹣2n+1+47<0 成立的正整数n的最小值.
,Sn=b1+b2+…bn , 求使 Sn﹣2n+1+47<0 成立的正整数n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的![]() 分别为14,18,则输出的
分别为14,18,则输出的![]() 为( )
为( )
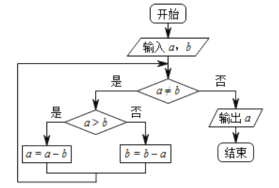
A. 0 B. 2 C. 4 D. 14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com