
已知 ,其中
,其中 是常数.
是常数.
(1)若 是奇函数,求
是奇函数,求 的值;
的值;
(2)求证: 的图像上不存在两点A、B,使得直线AB平行于
的图像上不存在两点A、B,使得直线AB平行于 轴.
轴.
(1)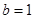 ;(2)证明见解析.
;(2)证明见解析.
解析试题分析:(1)奇函数的问题,可以根据奇函数的定义,利用 来解决,由于本题中有对数符号,有根式,因此根据
来解决,由于本题中有对数符号,有根式,因此根据 求出
求出 后,最好能再求出函数的定义域,验证下它是奇函数;(2)要证明函数
后,最好能再求出函数的定义域,验证下它是奇函数;(2)要证明函数 的图像上不存在两点A、B,使得直线AB平行于
的图像上不存在两点A、B,使得直线AB平行于 轴,即方程
轴,即方程 不可能有两个或以上的解,最多只有一个解,由于
不可能有两个或以上的解,最多只有一个解,由于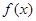 表达式不太简便,因此我们可以从简单的方面入手试试看,看
表达式不太简便,因此我们可以从简单的方面入手试试看,看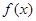 是不是单调函数,本题函数正好能根据单调性的定义证明此函数是单调函数,故本题结论得证.
是不是单调函数,本题函数正好能根据单调性的定义证明此函数是单调函数,故本题结论得证.
试题解析:(1)解法一:设 定义域为
定义域为 ,则:
,则:
因为 是奇函数,所以对任意
是奇函数,所以对任意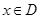 ,有
,有 , 3分
, 3分
得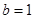 . 5分
. 5分
此时,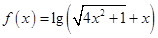 ,
, ,为奇函数。 6分
,为奇函数。 6分
解法二:当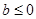 时,函数
时,函数 的定义域不关于原点对称,函数不是奇函数. 2分
的定义域不关于原点对称,函数不是奇函数. 2分
当 时,函数
时,函数 的定义域是一切实数. 3分
的定义域是一切实数. 3分
要使得函数是奇函数,则 对
对 成立。 5分
成立。 5分
所以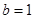 6分
6分
(2)设定义域内任意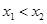 ,设
,设
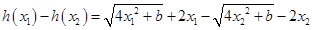

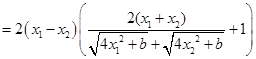 9分
9分
当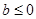 时,总有
时,总有 ,
,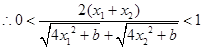 ,得
,得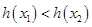 ; 11分
; 11分
当 时,
时,
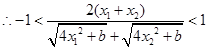 ,得
,得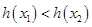 。
。
故总有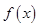 在定义域上单调递增 13分
在定义域上单调递增 13分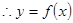 的图像上不存在两点,使得所连的直线与
的图像上不存在两点,使得所连的直线与 轴平行 14分
轴平行 14分
考点:(1)函数的奇偶性;(2)函数的单调性与方程的解.


科目:高中数学 来源: 题型:解答题
设V为全体平面向量构成的集合,若映射f:
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y= 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点 .
. 
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数f(x)=ax2+bx+1(a>0),F(x)= 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.
(1)求F(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.
(1)求实数a的值,并求函数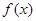 的单调区间,
的单调区间,
(2)若不等式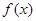 ≥k在区间
≥k在区间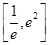 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 同时满足以下条件:
同时满足以下条件:
① 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;
② 是偶函数;
是偶函数;
③ 在x=0处的切线与直线
在x=0处的切线与直线 y=x+2垂直.
y=x+2垂直.
(1)求函数 =
= 的解析式;
的解析式;
(2)设g(x)= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< ,求实数m的取值范围..
,求实数m的取值范围..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com