
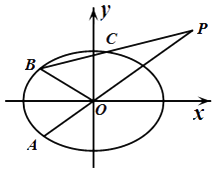
【题目】如图,在平面直角坐标系xOy中,已知椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() .A为椭圆上异于顶点的一点,点P满足
.A为椭圆上异于顶点的一点,点P满足 ![]() =
= ![]() ,
, 
(1)若点P的坐标为(2, ![]() ),求椭圆的方程;
),求椭圆的方程;
(2)设过点P的一条直线交椭圆于B,C两点,且 ![]() =m
=m ![]() ,直线OA,OB的斜率之积﹣
,直线OA,OB的斜率之积﹣ ![]() ,求实数m的值;
,求实数m的值;
(3)在(1)的条件下,是否存在定圆M,使得过圆M上任意一点T都能作出该椭圆的两条切线,且这两条切线互相垂直?若存在,求出定圆M;若不存在,说明理由.
【答案】
(1)解:由P(2, ![]() ),设A(x,y),则
),设A(x,y),则 ![]() =(2,
=(2, ![]() ),
), ![]() =(﹣x,﹣y),
=(﹣x,﹣y),
由题意可知: ![]() =
= ![]() ,
,
∴ ![]() ,则
,则 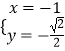 ,
,
A(﹣1,﹣ ![]() ),代入椭圆方程,得
),代入椭圆方程,得 ![]() ,
,
又椭圆的离心率e= ![]() =
= ![]() ,
,
则 ![]() =
= ![]() ,②
,②
由①②,得a2=2,b2=1,
故椭圆的方程为 ![]()
(2)解:设A(x1,y1),B(x2,y2),C(x3,y3),
∵ ![]() =
= ![]() ,
,
∴P(﹣2x1,﹣2y1),.
∵ ![]() =m
=m ![]() ,
,
∴(﹣2x1﹣x2,﹣2y1﹣y2)=m(x3﹣x2,y3﹣y2),
即 ![]() ,
,
于是 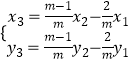 .
.
代入椭圆方程,得 ![]() +
+ ![]() =1,
=1,
![]() (
( ![]() )+
)+ ![]() (
( ![]() )﹣
)﹣ ![]() (
( ![]() +
+ ![]() )=1,
)=1,
∵A,B在椭圆上, ![]() ,
, ![]() ,
,
由直线OA,OB的斜率之积﹣ ![]() ,即
,即 ![]()
![]() =﹣
=﹣ ![]()
∴ ![]() ,
,
∴ ![]() ,解得:m=
,解得:m= ![]()
(3)解:存在定圆M,x2+y2=3,
在定圆M上任取一点T(x0,y0),其中x0≠± ![]() ,
,
设过点T(x0,y0)的椭圆的切线方程为y﹣y0=k(x﹣y0),即y=kx﹣kx0+y0,
∴ 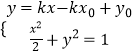 ,整理得:(1+2k2)x2﹣4k(﹣kx0+y0)x+2(﹣kx0+y0)2﹣2=0,
,整理得:(1+2k2)x2﹣4k(﹣kx0+y0)x+2(﹣kx0+y0)2﹣2=0,
由△=16k2(﹣kx0+y0)2﹣8(1+2k2)[(﹣kx0+y0)2﹣1]=0,
整理得:(2﹣ ![]() )k2+2kx0y0+1﹣
)k2+2kx0y0+1﹣ ![]() =0
=0
故过点T(x0,y0)的椭圆的两条切线斜率k1,k2分别是(2﹣ ![]() )k2+2kx0y0+1﹣
)k2+2kx0y0+1﹣ ![]() =0的两解.
=0的两解.
故k1k2= ![]() =
= ![]() =
= ![]() =﹣1,
=﹣1,
∴椭圆的两条切线垂直.
当x0=± ![]() 时,
时,
显然存在两条互相垂直的切线
【解析】(1)由题意可知: ![]() =
= ![]() ,求得A点坐标,由e=
,求得A点坐标,由e= ![]() =
= ![]() ,将A代入椭圆方程,即可求得a和b的值,求得椭圆的方程;(2)设A(x1 , y1),B(x2 , y2),C(x3 , y3),根据
,将A代入椭圆方程,即可求得a和b的值,求得椭圆的方程;(2)设A(x1 , y1),B(x2 , y2),C(x3 , y3),根据 ![]() =m
=m ![]() ,求得
,求得 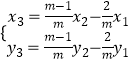 .代入椭圆方程
.代入椭圆方程 ![]() +
+ ![]() =1,由直线OA,OB的斜率之积﹣
=1,由直线OA,OB的斜率之积﹣ ![]() ,利用斜率公式求得
,利用斜率公式求得 ![]() ,代入整理得:
,代入整理得: ![]() ,解得:m=
,解得:m= ![]() ,;(3)假设存在否存在定圆M,求得直线的切线方程,代入椭圆方程,由△=0,求得(2﹣
,;(3)假设存在否存在定圆M,求得直线的切线方程,代入椭圆方程,由△=0,求得(2﹣ ![]() )k2+2kx0y0+1﹣
)k2+2kx0y0+1﹣ ![]() =0,则椭圆的两条切线斜率k1 , k2分别是(2﹣
=0,则椭圆的两条切线斜率k1 , k2分别是(2﹣ ![]() )k2+2kx0y0+1﹣
)k2+2kx0y0+1﹣ ![]() =0的两解,由韦达定理求得k1k2=
=0的两解,由韦达定理求得k1k2= ![]() =
= ![]() =
= ![]() =﹣1,因此椭圆的两条切线垂直,则当x0=±
=﹣1,因此椭圆的两条切线垂直,则当x0=± ![]() 时,显然存在两条互相垂直的切线,即可求得圆的方程.
时,显然存在两条互相垂直的切线,即可求得圆的方程.


科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元.它们与投入资金x万元的关系是:p= ![]() x,q=
x,q= ![]() .今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获取最大利润?最大利润为多少?
.今有3万元资金投入经营这两种商品,为获得最大利润,对这两种商品的资金分别投入多少时,能获取最大利润?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD的长AB=4,宽AD=3,将其沿对角线BD折起,得到四面体A﹣BCD,如图所示,给出下列结论:
①四面体A﹣BCD体积的最大值为 ![]() ;
;
②四面体A﹣BCD外接球的表面积恒为定值;
③若E、F分别为棱AC、BD的中点,则恒有EF⊥AC且EF⊥BD;
④当二面角A﹣BD﹣C为直二面角时,直线AB、CD所成角的余弦值为 ![]() ;
;
⑤当二面角A﹣BD﹣C的大小为60°时,棱AC的长为 ![]() .
.
其中正确的结论有(请写出所有正确结论的序号).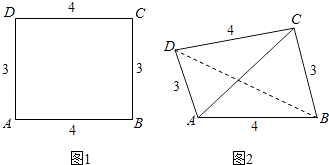
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了迎接青奥会,南京将在主干道统一安装某种新型节能路灯,该路灯由灯柱和支架组成.在如图所示的直角坐标系中,支架ACB是抛物线y2=2x的一部分,灯柱CD经过该抛物线的焦点F且与路面垂直,其中C在抛物线上,B为抛物线的顶点,DH表示道路路面,BF∥DH,A为锥形灯罩的顶,灯罩轴线与抛物线在A处的切线垂直.安装时要求锥形灯罩的顶到灯柱的距离是1.5米,灯罩的轴线正好通过道路路面的中线. 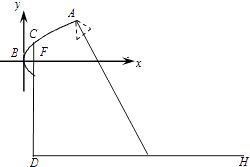
(1)求灯罩轴线所在的直线方程;
(2)若路宽为10米,求灯柱的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+φ)(ω>0),x=﹣ ![]() 是y=f(x)的零点,直线x=
是y=f(x)的零点,直线x= ![]() 为y=f(x)图象的一条对称轴,且函数f(x)在区间(
为y=f(x)图象的一条对称轴,且函数f(x)在区间( ![]() ,
, ![]() )上单调,则ω的最大值是( )
)上单调,则ω的最大值是( )
A.9
B.7
C.5
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点M,N分别是正方体ABCD﹣A1B1C1D1的棱BB1和B1C1的中点,则MN和CD1所成角的大小为( )
A.30°
B.60°
C.90°
D.120°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0,
=1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0, ![]() ),则e的取值范围是 .
),则e的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线与抛物线y2=2px(p>0)交于A,B两点,且OA⊥OB,OD⊥AB交AB于点D(不为原点).
(Ⅰ)求点D的轨迹方程;
(Ⅱ)若点D坐标为(2,1),求p的值.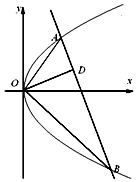
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体OABC﹣O′A′B′C′中,E,F分别是棱AB,BC上的动点. 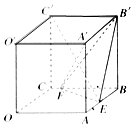
(1)当AE=BF时,求证A′F⊥C′E;
(2)若E,F分别为AB,BC的中点,求直线O′B与平面B′EF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com