
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,且满足
,且满足![]() .
.

(1)若直线![]() 的斜率为1,求点
的斜率为1,求点![]() 的坐标;
的坐标;
(2)若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该几何体的体积为_____,其外接球的表面积为______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年我省将实施新高考,新高考“依据统一高考成绩、高中学业水平考试成绩,参考高中学生综合素质评价信息”进行人才选拔。我校2018级高一年级一个学习兴趣小组进行社会实践活动,决定对某商场销售的商品A进行市场销售量调研,通过对该商品一个阶段的调研得知,发现该商品每日的销售量![]() (单位:百件)与销售价格
(单位:百件)与销售价格![]() (元/件)近似满足关系式
(元/件)近似满足关系式![]() ,其中
,其中![]() 为常数
为常数![]() 已知销售价格为3元/件时,每日可售出该商品10百件。
已知销售价格为3元/件时,每日可售出该商品10百件。
(1)求函数![]() 的解析式;
的解析式;
(2)若该商品A的成本为2元/件,根据调研结果请你试确定该商品销售价格的值,使该商场每日销售该商品所获得的利润(单位:百元)最大。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,离心率为
,离心率为![]() .
.
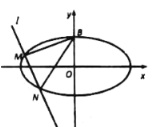
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭园C交于
与椭园C交于![]() ,
,![]() 两点,直线
两点,直线![]() 与线
与线![]() 的斜率之积为
的斜率之积为![]() ,证明:直线
,证明:直线![]() 过定点,并求
过定点,并求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点![]() ,点
,点![]() 均在圆
均在圆![]() 上,且
上,且![]() ,过点
,过点![]() 作
作![]() 的平行线分别交
的平行线分别交![]() ,
,![]() 于
于![]() 两点.
两点.
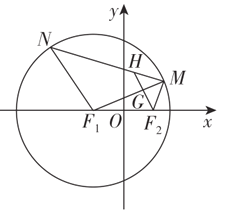
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹交于
的轨迹交于![]() 两点.问是否存在常数
两点.问是否存在常数![]() ,使得
,使得![]() 点为定值?若存在,求出
点为定值?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点A
过点A![]() ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com