
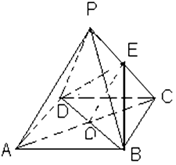
 如图四棱锥P-ABCD,四边形ABCD是正方形,O是正方形的中心,E是PC的中点,且PA=AB=PB.
如图四棱锥P-ABCD,四边形ABCD是正方形,O是正方形的中心,E是PC的中点,且PA=AB=PB.分析 (1)连接OE,易证OE∥AP,得PA∥平面BDE
(2)作BC的中点M并且连接OM,得∠EOM(或补角)就是EO与AB所成的角,解△OME 即可,
解答 解:(1)证明:连接OE,∵O是正方形的中心,E是PC的中点,
易证OE∥AP,OE?平面BDE,AP?平面BDE,得PA∥平面BDE;
(2)作BC的中点M并且连接OM,
得 AB∥OM,∴∠EOM(或补角)就是EO与AB所成的角;
∵四边形ABCD是正方形,PA=AB=PB,得△OME为等边三角形,
∴∠EOM=60°
则异面直线所成角为60°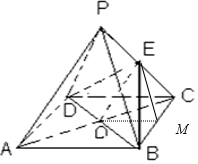
点评 本题考查了线面平行,及异面直线的夹角,空间问题转化为平面几何问题是关键,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
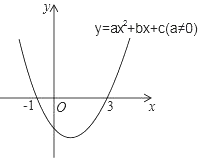 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0;②当-1≤x≤3时,y<0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0其中正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0;②当-1≤x≤3时,y<0;③若(x1,y1)、(x2,y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0其中正确的是( )| A. | ①②④ | B. | ①④ | C. | ①②③ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
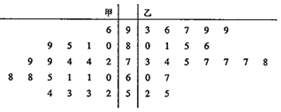
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
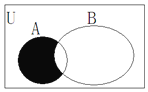
| A. | (-1,1) | B. | [-1,1] | C. | [1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com