Question

【题目】设事件A表示“关于的一元二次方程有实根”，其中， 为实常数.

（Ⅰ）若为区间[0，5]上的整数值随机数， 为区间[0，2]上的整数值随机数，求事件A发生的概率；

（Ⅱ）若为区间[0，5]上的均匀随机数， 为区间[0，2]上的均匀随机数，求事件A发生的概率.

Answer 1

【答案】（Ⅰ）;（Ⅱ）.

【解析】试题分析：

(1)列出所有可能的事件，结合古典概型公式可得满足题意的概率值为；

(2)利用题意画出概率空间，结合几何概型公式可得满足题意的概率值为.

试题解析：

（Ⅰ）当a∈{0，1，2，3，4，5}，b∈{0，1，2}时，共可以产生6×3=18个一元二次方程.

若事件A发生，则a 2－4b2≥0，即|a|≥2|b|. 又a≥0， b≥0，所以a≥2b.

从而数对（a，b）的取值为（0，0），（1，0），（2，0），（2，1），（3，0），（3，1），（4，0），（4，1），（4，2），（5，0），（5，1），（5，2），共12组值.

所以P（A）=.

（Ⅱ）据题意，试验的全部结果所构成的区域为D={(a，b)|0≤a≤5，0≤b≤2}，构成事件A的区域为A={(a，b)|0≤a≤5，0≤b≤2，a≥2b}.

在平面直角坐标系中画出区域A、D，如图，

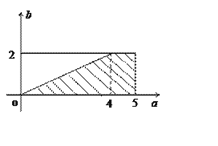
其中区域D为矩形，其面积S（D）=5×2=10，

区域A为直角梯形，其面积S（A）=.

所以P（A）=.