
【题目】已知椭圆![]() 的左.右焦点为
的左.右焦点为![]() ,离心率为
,离心率为![]() .直线
.直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,设
的对称点,设![]() .
.
(1)证明:![]() ;
;
(2)若![]() ,
,![]() 的周长为
的周长为![]() ;写出椭圆
;写出椭圆![]() 的方程;
的方程;
(3)确定![]() 的值,使得
的值,使得![]() 是等腰三角形.
是等腰三角形.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱台![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.

(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() //平面
//平面![]() ;
;
(2)棱BC上是否存在一点E,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求线段CE的长;若不存在,请说明理由.
?若存在,求线段CE的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校对甲、乙两个班级的同学进行了体能测验,成绩统计如下(每班50人):

(1)成绩不低于80分记为“优秀”.请填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“成绩优秀”与所在教学班级有关?
的把握认为“成绩优秀”与所在教学班级有关?

(2)从两个班级的成绩在![]() 的所有学生中任选2人,其中,甲班被选出的学生数记为
的所有学生中任选2人,其中,甲班被选出的学生数记为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
赋:![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部最新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米。某城市环保部分随机抽取的一居民区过去20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
组别 | PM2.5平均浓度 | 频数 | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(II)求样本平均数,并根据样本估计总计的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,它在点
,它在点![]() 处的切线为直线
处的切线为直线![]() .
.
(I)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 为椭圆
为椭圆![]() 上一点,求点
上一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过抛物线上一点
,过抛物线上一点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)判断![]() 的形状;
的形状;
(2) 若![]() 两点在抛物线
两点在抛物线![]() 上,点
上,点![]() 满足
满足![]() ,若抛物线
,若抛物线![]() 上存在异于
上存在异于![]() 的点
的点![]() ,使得经过
,使得经过![]() 三点的圆与抛物线在点
三点的圆与抛物线在点![]() 处的有相同的切线,求点
处的有相同的切线,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】必修四第一章我们借助圆的对称性学习了诱导公式,如![]() 在直观上讲单位圆中,当两个角的终边关于
在直观上讲单位圆中,当两个角的终边关于![]() 轴对称时,这两个角的正弦值相等;再如
轴对称时,这两个角的正弦值相等;再如![]() 在单位圆中,当两个角的终边关于原点中心对称时,这两个角的正弦值互为相反数.观察这些诱导公式,可以发现它们都是特殊角与任意角
在单位圆中,当两个角的终边关于原点中心对称时,这两个角的正弦值互为相反数.观察这些诱导公式,可以发现它们都是特殊角与任意角![]() 的三角函数的恒等关系.我们如果将特殊角换为任意角
的三角函数的恒等关系.我们如果将特殊角换为任意角![]() ,那么任意角
,那么任意角![]() 与
与![]() 的和(或差)的三角函数与
的和(或差)的三角函数与![]() ,
,![]() 的三角函数会有什么关系呢?如果已知
的三角函数会有什么关系呢?如果已知![]() ,
,![]() 的正弦余弦,能由此推出
的正弦余弦,能由此推出![]() 的正弦余弦吗?下面是某高一学生在老师的指导下自行探究
的正弦余弦吗?下面是某高一学生在老师的指导下自行探究![]() 与角
与角![]()
![]() 的正弦余弦之间的关系的部分过程,请你顺着这位同学的思路以及老师的提示将探究过程完善,并完成后面的题目.探究过程如下:
的正弦余弦之间的关系的部分过程,请你顺着这位同学的思路以及老师的提示将探究过程完善,并完成后面的题目.探究过程如下:
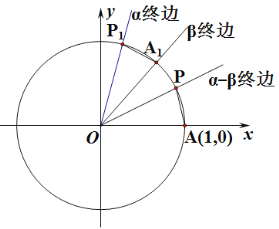
不妨令![]() 如图,设单位圆与
如图,设单位圆与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() 以
以![]() 轴的非负半轴为始边作角
轴的非负半轴为始边作角![]() 它们的终边分别与单位圆相交于点
它们的终边分别与单位圆相交于点![]() 连接
连接![]() 若把扇形
若把扇形![]() 绕着点
绕着点![]() 旋转
旋转![]() 角,则点
角,则点![]() 分别与点
分别与点![]() 重合. ……(未完待续)
重合. ……(未完待续)
(提示一:任意一个圆绕着其圆心旋转任意角后都与原来的圆重合,这一性质叫做圆的旋转对称性)(提示二:平面上任意两点![]() 间的距离公式
间的距离公式![]() )
)
(1)完善上述探究过程;
(2)利用(1)中的结论解决问题:已知![]()
![]() 是第三象限角,求
是第三象限角,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某盒子内装有三种颜色的玻璃球,一位同学每次从中随机拿出一个玻璃球,观察颜色后再放回,重复了50次,得到的信息如下:观察到红色26次、蓝色13次.如果从这个盒子内任意取一个玻璃球,估计:
(1)这个球既不是红色也不是蓝色的概率;
(2)这个球是红色或者是蓝色的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com