
【题目】某产品的广告支出x(单位:万元)与销售收入y(单位:万元)之间有下表所对应的数据:
广告支出x(单位:万元) | 1 | 2 | 3 | 4 |
销售收入y(单位:万元) | 12 | 28 | 42 | 56 |
(1)画出表中数据的散点图;
(2)求出y对x的回归直线方程![]() ;
;
(3)若广告费为9万元,则销售收入约为多少万元?
参考公式: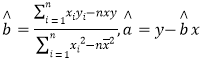
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】等比数列{an}的各项均为正数,且a2=2,a4=![]() .
.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]()
(3)试预测加工10个零件需要多少小时?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
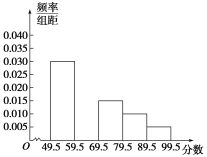
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数是多少?
(3)求这两个班参赛学生的成绩的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)![]() 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求![]() 的分布列与数学期望.
的分布列与数学期望.
(注:若三个数![]() 满足
满足![]() ,则称
,则称![]() 为这三个数的中位数).
为这三个数的中位数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数
f(x)=(cosx﹣x)(π+2x)﹣ ![]() (sinx+1)
(sinx+1)
g(x)=3(x﹣π)cosx﹣4(1+sinx)ln(3﹣ ![]() )
)
证明:
(1)存在唯一x0∈(0, ![]() ),使f(x0)=0;
),使f(x0)=0;
(2)存在唯一x1∈( ![]() ,π),使g(x1)=0,且对(Ⅰ)中的x0 , 有x0+x1<π.
,π),使g(x1)=0,且对(Ⅰ)中的x0 , 有x0+x1<π.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆C:![]() (a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为![]() ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com