
【题目】已知函数![]() 的部分图象如图所示,且相邻的两个最值点的距离为
的部分图象如图所示,且相邻的两个最值点的距离为![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 的图象向左平移1个单位长度后得到函数
的图象向左平移1个单位长度后得到函数![]() 的图象,关于
的图象,关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围.
的取值范围.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,离心率为
,离心率为![]() .
.
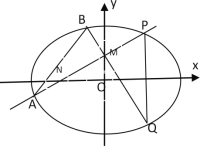
(1)求椭圆![]() 的方程;
的方程;
(2)过动点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,
,![]() (
(![]() 在第一象限),且
在第一象限),且![]() 是线段
是线段![]() 的中点.过点
的中点.过点![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于另一点
于另一点![]() ,延长
,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
①设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,证明
,证明![]() 为定值;
为定值;
②求直线![]() 斜率取最小值时,直线
斜率取最小值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于项数为![]() (
(![]() )的有穷正整数数列
)的有穷正整数数列![]() ,记
,记![]() (
(![]() ),即
),即![]() 为
为![]() 中的最大值,称数列
中的最大值,称数列![]() 为数列
为数列![]() 的“创新数列”.比如
的“创新数列”.比如![]() 的“创新数列”为
的“创新数列”为![]() .
.
(1)若数列![]() 的“创新数列”
的“创新数列”![]() 为1,2,3,4,4,写出所有可能的数列
为1,2,3,4,4,写出所有可能的数列![]() ;
;
(2)设数列![]() 为数列
为数列![]() 的“创新数列”,满足
的“创新数列”,满足![]() (
(![]() ),求证:
),求证: ![]() (
(![]() );
);
(3)设数列![]() 为数列
为数列![]() 的“创新数列”,数列
的“创新数列”,数列![]() 中的项互不相等且所有项的和等于所有项的积,求出所有的数列
中的项互不相等且所有项的和等于所有项的积,求出所有的数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() 、
、![]() 、
、![]() 、
、![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说:“![]() 、
、![]() 同时获奖.”
同时获奖.”
乙说:“![]() 、
、![]() 不可能同时获奖.”
不可能同时获奖.”
丙说:“![]() 获奖.”
获奖.”
丁说:“![]() 、
、![]() 至少一件获奖”
至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的金秋十月,越野e族阿拉善英雄会在内蒙古自治区阿拉善盟阿左旗腾格里沙漠举行,该项目已打造成集沙漠竞技运动、汽车文化极致体验、主题休闲度假为一体的超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数![]() (万人)与沙漠中所需环保车辆数量
(万人)与沙漠中所需环保车辆数量![]() (辆),得到如下统计表:
(辆),得到如下统计表:
参会人数 | 11 | 9 | 8 | 10 | 12 |
所需环保车辆 | 28 | 23 | 20 | 25 | 29 |
(1)根据统计表所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知租用的环保车平均每辆的费用![]() (元)与数量
(元)与数量![]() (辆)的关系为
(辆)的关系为
![]() .主办方根据实际参会人数为所需要投入使用的环保车,
.主办方根据实际参会人数为所需要投入使用的环保车,
每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润![]() 是多少?(注:利润
是多少?(注:利润![]() 主办方支付费用
主办方支付费用![]() 租用车辆的费用).
租用车辆的费用).
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通拥堵指数是综合反映道路网畅通或拥堵的概念,记交通拥堵指数为 ,其范围为 ![]() ,分别有五个级别: 畅通; 基本畅通; 轻度拥堵; 中度拥堵;
,分别有五个级别: 畅通; 基本畅通; 轻度拥堵; 中度拥堵; ![]() 严重拥堵.晚高峰时段
严重拥堵.晚高峰时段 ![]() ,从某市交通指挥中心选取了市区
,从某市交通指挥中心选取了市区 ![]() 个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示.
个交通路段,依据其交通拥堵指数数据绘制的直方图如图所示.
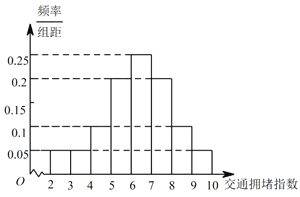
(Ⅰ)求出轻度拥堵,中度拥堵,严重拥堵路段各有多少个;
(Ⅱ)用分层抽样的方法从交通指数在 ![]() ,
, ![]() ,
, ![]() 的路段中共抽取
的路段中共抽取![]() 个路段,求依次抽取的三个级别路段的个数;
个路段,求依次抽取的三个级别路段的个数;
(Ⅲ)从(Ⅱ)中抽取的![]() 个路段中任取
个路段中任取![]() 个,求至少
个,求至少![]() 个路段为轻度拥堵的概率.
个路段为轻度拥堵的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com